最小二乘法是用来做函数拟合或者求函数极值的方法。在机器学习,尤其是回归模型中,经常可以看到最小二乘法的身影 。
1.最小二乘法的原理与要解决的问题
最小二乘法是由勒让德在19世纪发现的,原理的一般形式很简单,当然发现的过程是非常艰难的。形式如下式:
\[目标函数 = \sum\limits(观测值-理论值)^2\]观测值就是我们的多组样本,理论值就是我们的假设拟合函数。目标函数也就是在机器学习中常说的损失函数,我们的目标是得到使目标函数最小化时候的拟合函数的模型。举一个最简单的线性回归的简单例子,比如我们有m个只有一个特征的样本:
\[(x^{(1)},y^{(1)}), (x^{(2)},y^{(2)},...(x^{(m)},y^{(m)})\]样本采用下面的拟合函数:
\[h_\theta(x) = \theta_0 + \theta_1 x\]这样我们的样本有一个特征x,对应的拟合函数有两个参数 \(θ_0\) 和 \(θ_1\) 需要求出。
我们的目标函数为:
\[J(\theta_0, \theta_1) = \sum\limits_{i=1}^{m}(y^{(i)} - h_\theta(x^{(i)})^2 = \sum\limits_{i=1}^{m}(y^{(i)} - \theta_0 - \theta_1 x^{(i)})^2\]用最小二乘法做什么呢,使 \(J(θ0,θ1)\) 最小,求出使\(J(θ0,θ1)\)最小时的 \(θ_0\) 和 \(θ_1\) ,这样拟合函数就得出了。
2.最小二乘法的代数法解法
上面提到要使 \(J(θ0,θ1)\) 最小,方法就是对 \(θ_0\) 和 \(θ_1\) 分别来求偏导数,令偏导数为0,得到一个关于 \(θ_0\) 和 \(θ_1\) 的二元方程组。求解这个二元方程组,就可以得到 \(θ_0\) 和 \(θ_1\) 的值。下面我们具体看看过程。
\(J(\theta_0, \theta_1)对\theta_0\) 求导,得到如下方程:
\[\sum\limits_{i=1}^{m}(y^{(i)} - \theta_0 - \theta_1 x^{(i)}) = 0\]\(J(\theta_0, \theta_1)对\theta_1\) 求导,得到如下方程:
\[\sum\limits_{i=1}^{m}(y^{(i)} - \theta_0 - \theta_1 x^{(i)})x^{(i)} = 0\]组成一个二元一次方程组,容易求出 \(θ_0\) 和 \(θ_1\) 的值:
\[\theta_0 = \sum\limits_{i=1}^{m}\big(x^{(i)})^2\sum\limits_{i=1}^{m}y^{(i)} - \sum\limits_{i=1}^{m}x^{(i)}\sum\limits_{i=1}^{m}x^{(i)}y^{(i)} \Bigg/ m\sum\limits_{i=1}^{m}\big(x^{(i)})^2 - \big(\sum\limits_{i=1}^{m}x^{(i)})^2\] \[\theta_1 = m\sum\limits_{i=1}^{m}x^{(i)}y^{(i)} - \sum\limits_{i=1}^{m}x^{(i)}\sum\limits_{i=1}^{m}y^{(i)} \Bigg/ m\sum\limits_{i=1}^{m}\big(x^{(i)})^2 - \big(\sum\limits_{i=1}^{m}x^{(i)})^2\]这个方法很容易推广到多个样本特征的线性拟合。
拟合函数表示为 \(h_\theta(x_1, x_2, ...x_n) = \theta_0 + \theta_{1}x_1 + ... + \theta_{n}x_{n}\) , 其中 \(\theta_i (i = 0,1,2... n)\) 为模型参数,\(x_i\) (i = 0,1,2… n)为每个样本的 n 个特征值。这个表示可以简化,我们增加一个特征 \(x_0 = 1\) ,这样拟合函数表示为:
\[h_\theta(x_0, x_1, ...x_n) = \sum\limits_{i=0}^{n}\theta_{i}x_{i}\]损失函数表示为:
\[J(\theta_0, \theta_1..., \theta_n) = \sum\limits_{j=1}^{m}(h_\theta(x_0^{(j)}), x_1^{(j)}, ...x_n^{(j)})) - y^{(j)}))^2 = \sum\limits_{j=1}^{m}(\sum\limits_{i=0}^{n}\theta_{i}x_{i}^{(j)}- y^{(j)})^2\]利用损失函数分别对 \(θ_i\)(i=0,1,…n)求导,并令导数为0可得:
\[\sum\limits_{j=0}^{m}(\sum\limits_{i=0}^{n}(\theta_{i}x_{i}^{(j)} - y^{(j)})x_i^{(j)}= 0 \qquad(i=0,1,...n)\]这样我们得到一个N+1元一次方程组,这个方程组有N+1个方程,求解这个方程,就可以得到所有的N+1个未知的\(θ\) 。
3.最小二乘法的矩阵法解法
矩阵法比代数法要简洁,且矩阵运算可以取代循环,所以现在很多书和机器学习库都是用的矩阵法来做最小二乘法。
这里用上面的多元线性回归例子来描述矩阵法解法。
假设函数 \(h_\theta(x_1, x_2, ...x_n) = \theta_0 + \theta_{1}x_1 + ... + \theta_{n-1}x_{n-1}\) 的矩阵表达方式为:
\[h_\mathbf{\theta}(\mathbf{x}) = \mathbf{X\theta}\]其中, 假设函数 \(h_\mathbf{\theta}(\mathbf{X})\) 为 \(m \times 1\) 的向量, \(\mathbf{\theta}\) 为 \(n \times 1\)的向量, 里面有n个代数法的模型参数。\(\mathbf{X}\) 为 \(m \times n\) 维的矩阵。m 代表样本的个数,n 代表样本的特征数。
损失函数定义为:
\[J(\mathbf\theta) = \frac{1}{2}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y})\] \[\|A x-b\|_{2}^{2}=(A x-b)^{T} *(A x-b)\]其中 \(\mathbf{Y}\) 是样本的输出向量,维度为 \(m \times 1\). \(1 / 2\)在这主要是为了求导后系数为1,方便计算。
根据最小二乘法的原理,我们要对这个损失函数对 \(\mathbf{\theta}\) 向量求导取 0。结果如下式:
\[\frac{\partial}{\partial\mathbf\theta}J(\mathbf\theta) = \mathbf{X}^T(\mathbf{X\theta} - \mathbf{Y}) = 0\]这里面用到了矩阵求导链式法则,和两个个矩阵求导的公式。
公式1:\(\frac{\partial}{\partial\mathbf{x}}(\mathbf{x^Tx}) =2\mathbf{x}\;\;x为向量\)
公式2:\(\nabla_Xf(AX+B) = A^T\nabla_Yf,\;\; Y=AX+B,\;\;f(Y)为标量\)
对上述求导等式整理后可得:
\[\mathbf{X^{T}X\theta} = \mathbf{X^{T}Y}\]两边同时左乘 \((\mathbf{X^{T}X})^{-1}\) 可得:
\[\mathbf{\theta} = (\mathbf{X^{T}X})^{-1}\mathbf{X^{T}Y}\]这样我们就一下子求出了 \(\theta\) 向量表达式的公式,免去了代数法一个个去求导的麻烦。只要给了数据,我们就可以用 \(\mathbf{\theta} = (\mathbf{X^{T}X})^{-1}\mathbf{X^{T}Y}\) 算出 \(\theta\)。
4.最小二乘法的局限性和适用场景
从上面可以看出,最小二乘法适用简洁高效,比梯度下降这样的迭代法似乎方便很多。但是这里我们就聊聊最小二乘法的局限性。
首先,最小二乘法需要计算 \(\mathbf{X^{T}X}\) 的逆矩阵,有可能它的逆矩阵不存在,这样就没有办法直接用最小二乘法了,此时梯度下降法仍然可以使用。当然,我们可以通过对样本数据进行整理,去掉冗余特征。让 \(\mathbf{X^{T}X}\) 的行列式不为0,然后继续使用最小二乘法。
第二,当样本特征 n 非常的大的时候,计算 \(\mathbf{X^{T}X}\) 的逆矩阵是一个非常耗时的工作(nxn的矩阵求逆),甚至不可行。此时以梯度下降为代表的迭代法仍然可以使用。那这个n到底多大就不适合最小二乘法呢?如果你没有很多的分布式大数据计算资源,建议超过10000个特征就用迭代法吧。或者通过主成分分析降低特征的维度后再用最小二乘法。
第三,如果拟合函数不是线性的,这时无法使用最小二乘法,需要通过一些技巧转化为线性才能使用,此时梯度下降仍然可以用。
第四,讲一些特殊情况。当样本量m很少,小于特征数n的时候,这时拟合方程是欠定的,常用的优化方法都无法去拟合数据。当样本量m等于特征数n的时候,用方程组求解就可以了。当m大于n时,拟合方程是超定的,也就是我们常用与最小二乘法的场景了。
python code
\[\mathbf{\theta} = (\mathbf{X^{T}X})^{-1}\mathbf{X^{T}Y}\]import numpy as np
import matplotlib.pyplot as plt
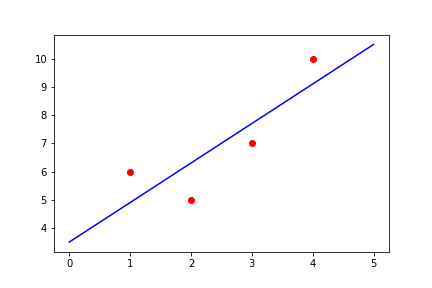
data = np.array([
[1, 6],
[2, 5],
[3, 7],
[4, 10]
])
m = len(data)
X = np.array([np.ones(m), data[:, 0]]).T
y = np.array(data[:, 1]).reshape(-1, 1)
W = np.linalg.solve(X.T.dot(X), X.T.dot(y)) ## 求解 XW=y的值,W
##show
plt.figure(1)
xx = np.linspace(0, 5, 2)
yy = np.array(W[0] + W[1] * xx)
plt.plot(xx, yy.T, color='b')
plt.scatter(data[:, 0], data[:, 1], color='r')
plt.show()
numpy.linalg.solve(a, b) 以矩阵形式解一个线性矩阵方程,或线性标量方程组。
参数:
- a-系数矩阵
- b-纵坐标或因变量的值
返回值
- x-方程组ax=b的解,shape与b一样