损失函数
损失函数和代价函数是同一个东西,目标函数是一个与他们相关但更广的概念,对于目标函数来说在有约束条件下的最小化就是损失函数(loss function)。
举个例子解释一下:(图片来自Andrew Ng Machine Learning公开课视频)
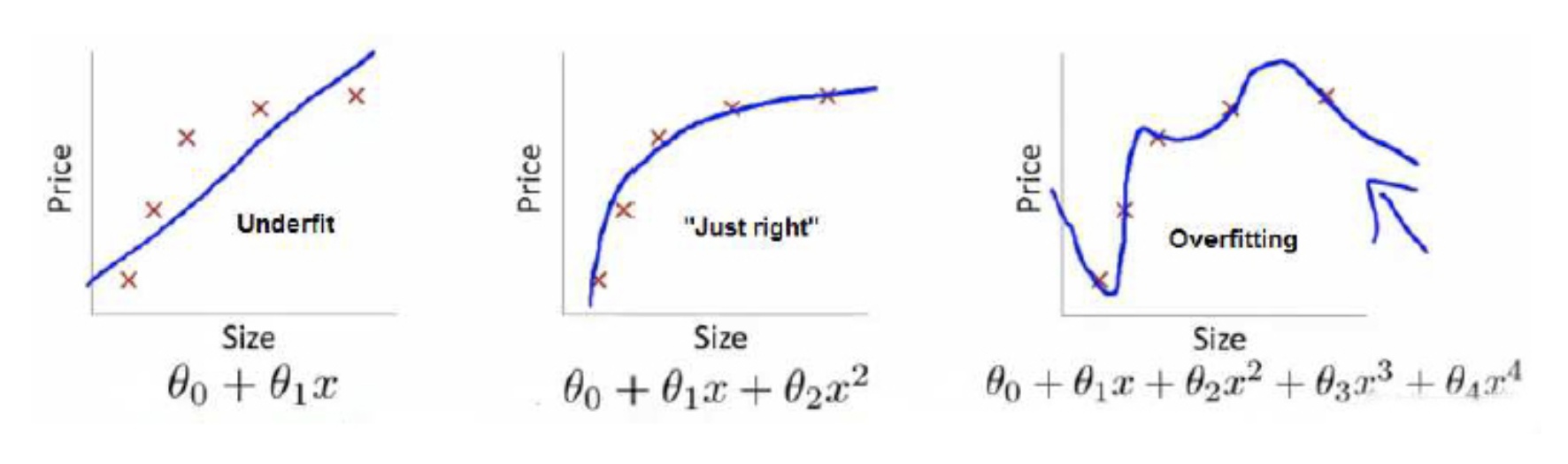
上面三个图的函数依次为 \(f_{1}(x), f_{2}(x), f_{3}(x)\) 。我们是想用这三个函数分别来拟合Price,Price的真实值记为 $Y$ 。
我们给定 $x$ ,这三个函数都会输出一个 $f(x)$ , 这个输出的 $f(x)$ 与真实值 $Y$ 可能是相同的,也可能是不同的,为了表示我们拟合的好坏,我们就用一个函数来度量拟合的程度,比如:
\[\begin{equation}L(Y, f(X))=\frac{1}{2} \sum_{i=1}^{N}(Y-f(X))^{2}\end{equation}\]个函数就称为损失函数(loss function),或者叫代价函数(cost function)。损失函数越小,就代表模型拟合的越好。损失函数为平方损失。系数 $\frac{1}{2}$ 为了计算方便
那是不是我们的目标就只是让loss function越小越好呢?还不是。
这个时候还有一个概念叫风险函数(risk function)。风险函数是损失函数的期望,这是由于我们输入输出的 遵循一个联合分布,但是这个联合分布是未知的,所以无法计算。但是我们是有历史数据的,就是我们的训练集,
关于训练集的平均损失称作经验风险(empirical risk),
即:
\[\begin{equation}\frac{1}{N} \sum_{i=1}^{N} L\left(y_{i}, f\left(x_{i}\right)\right)\end{equation}\]所以我们的目标就是最小化:
\[\begin{equation}\frac{1}{N} \sum_{i=1}^{N} L\left(y_{i}, f\left(x_{i}\right)\right)\end{equation}\]称为经验风险最小化。
到这里完了吗?还没有。
如果到这一步就完了的话,那我们看上面的图,那肯定是最右面的 的经验风险函数最小了,因为它对历史的数据拟合的最好嘛。但是我们从图上来看
肯定不是最好的,因为它过度学习历史数据,导致它在真正预测时效果会很不好,这种情况称为过拟合(over-fitting)。
为什么会造成这种结果?大白话说就是它的函数太复杂了,都有四次方了,这就引出了下面的概念,我们不仅要让经验风险最小化,还要让结构风险最小化。这个时候就定义了一个函数 ,这个函数专门用来度量模型的复杂度,在机器学习中也叫正则化(regularization)。常用的有
,
范数。
到这一步我们就可以说我们最终的优化函数是:
\[\begin{equation}\min \frac{1}{N} \sum_{i=1}^{N} L\left(y_{i}, f\left(x_{i}\right)\right)+\lambda J(f)\end{equation}\]即最优化经验风险和结构风险,而这个函数就被称为目标函数。
结合上面的例子来分析:最左面的 结构风险最小(模型结构最简单),但是经验风险最大(对历史数据拟合的最差);最右面的
经验风险最小(对历史数据拟合的最好),但是结构风险最大(模型结构最复杂);而
达到了二者的良好平衡,最适合用来预测未知数据集。
正则化
模型选择的典型方法是正则化( regularization)。正则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项( regularizer)或罚项( penalty term)。正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化值就越大。比如,正则化项可以是模型参数向量的范数。
正则化一般具有如下形式:
\[\begin{equation}\min _{f \in \mathcal{F}} \frac{1}{N} \sum_{i=1}^{N} L\left(y_{i}, f\left(x_{i}\right)\right)+\lambda J(f)\end{equation}\]其中,第1项是经验风险,第2项是正则化项,$\lambda $≥0为调整两者之间关系的系数。 正则化项可以取不同的形式。例如,回归问题中,损失函数是平方损失,正则化项可以是参数向量的$L2$范数:
\[\begin{equation}L(w)=\frac{1}{N} \sum_{i=1}^{N}\left(f\left(x_{i} ; w\right)-y_{i}\right)^{2}+\frac{\lambda}{2}\|w\|^{2}\end{equation}\]| $w$ 表示参数向量,这里 $$ | w | 表示参数向量w的 L_2 范数$$ |
正则化也可以是参数向量 $L_1$ 范数
\[\begin{equation}L(w)=\frac{1}{N} \sum_{i=1}^{N}\left(f\left(x_{i} ; w\right)-y_{i}\right)^{2}+{\lambda}\|w\|_{1}\end{equation}\]| 这里,$$ | w | _1 表示参数向量w的 L_1 范数$$ |
范数
以下分别列举常用的向量范数和矩阵范数的定义。
向量范数
-
1-范数:即向量元素绝对值之和, \(\|x\|_{1}=\sum_{i=1}^{N}\left|x_{i}\right|\)
-
2-范数:Euclid范数(欧几里得范数,常用计算向量长度),即向量元素绝对值的平方和再开方。
\[\|\mathbf{x}\|_{2}=\sqrt{\sum_{i=1}^{N} x_{i}^{2}}\] -
$\infty$-范数 : 即所有向量元素绝对值中的最大值
\[\|\mathbf{x}\|_{\infty}=\max _{i}\left|x_{i}\right|\] -
$-\infty$-范数 : 即所有向量元素绝对值中的最小值 。
-
p-范数:即向量元素绝对值的p次方和的1/p次幂
\[\|\mathbf{x}\|_{p}=\left(\sum_{i=1}^{N}\left|x_{i}\right|^{p}\right)^{\frac{1}{p}}\]
矩阵范数
-
1-范数: 列和范数,即所有矩阵列向量绝对值之和的最大值 。 \(\|A\|_{1}=\max _{j} \sum_{i=1}^{m}\left|a_{i, j}\right|\)
-
2-范数:谱范数,即 $A^TA$ 矩阵的最大特征值的开平方。
\(\|A\|_{2}=\sqrt{\lambda_{1}}\) $\lambda$ 为 $A^{T} A$ 的最大特征值。
- $\infty$ - 范数 : 行和范数,即所有矩阵行向量绝对值之和的最大值 。 \(\|A\|_{\infty}=\max _{i} \sum_{j=1}^{N}\left|a_{i, j}\right|\)
- F-范数:Frobenius范数,即矩阵元素绝对值的平方和再开平方 。
- 核范数:$ \lambda_{i}$ 是A的奇异值 。即奇异值之和。
$L_p$ 范数是常用的正则化项,其中 $L_2$ 范数$||w||_2$倾向于w 的分量取值尽量均衡,即非零分量个数尽量稠密,而 $L_0$ 范数与 $L_1$ 范数则是倾向于w的分量尽量稀疏,即非零分量个数尽量少 。