Python常用数据结构之 heapq 模块

主要函数
- 基本函数
- 基于堆的通用功能函数。
常用方法示例
堆排序示例
参考：

这个模块提供了堆队列算法的实现，也称为优先队列算法。

heapq 模块实现了一个适用于 Python 列表的最小堆排序算法。

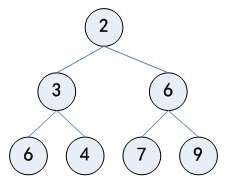
堆是一个二叉树，它的每个父节点的值都只会小于或大于所有孩子节点（的值）。它使用了数组来实现：从零开始计数，对于所有的 k ，都有 heap[k] <= heap[2*k+1] 和 heap[k] <= heap[2*k+2]。为了便于比较，不存在的元素被认为是无限大。堆最有趣的特性在于最小的元素总是在根结点：heap[0]。

这个API与教材的堆算法实现有所不同，具体区别有两方面：

使用了从零开始的索引。这使得节点和其孩子节点索引之间的关系不太直观但更加适合，因为 Python 使用从零开始的索引。
pop 方法返回最小的项而不是最大的项（这在教材中称为“最小堆”；而“最大堆”在教材中更为常见，因为它更适用于原地排序）。

Python的 heapq 模块实现了一个最小堆。

基于这两方面，把堆看作原生的Python list也没什么奇怪的： heap[0] 表示最小的元素，同时 heap.sort() 维护了堆的不变性！

主要函数

基本函数

heapq.heappush(heap, item)
将 item 的值加入 heap 中，保持堆的不变性。
heapq.heappop(heap) 弹出并返回 heap 的最小的元素，保持堆的不变性。如果堆为空，抛出 IndexError 。使用 heap[0] ，可以只访问最小的元素而不弹出它。
heapq.heappushpop(heap, item) 将 item 放入堆中，然后弹出并返回 heap 的最小元素。该组合操作比先调用 heappush() 再调用 heappop() 运行起来更有效率。
heapq.heapify(x) 将 list x 转换成堆，原地，线性时间内。
heapq.heapreplace(heap, item) 弹出并返回 heap 中最小的一项，同时推入新的 item。堆的大小不变。如果堆为空则引发 IndexError。这个单步骤操作比 heappop() 加 heappush() 更高效，并且在使用固定大小的堆时更为适宜。 pop/push 组合总是会从堆中返回一个元素并将其替换为 item。返回的值可能会比添加的 item 更大。如果不希望如此，可考虑改用 heappushpop()。它的 push/pop 组合会返回两个值中较小的一个，将较大的值留在堆中。

基于堆的通用功能函数。

heapq.merge(*iterables, key=None, reverse=False) 将多个已排序的输入合并为一个已排序的输出（例如，合并来自多个日志文件的带时间戳的条目）。返回已排序值的 iterator。类似于 sorted(itertools.chain(*iterables)) 但返回一个可迭代对象，不会一次性地将数据全部放入内存，并假定每个输入流都是已排序的（从小到大）。

具有两个可选参数，它们都必须指定为关键字参数。

key 指定带有单个参数的 key function，用于从每个输入元素中提取比较键。默认值为 None (直接比较元素)。

reverse 为一个布尔值。如果设为 True，则输入元素将按比较结果逆序进行合并。要达成与 sorted(itertools.chain(*iterables), reverse=True) 类似的行为，所有可迭代对象必须是已从大到小排序的。
heapq.nlargest(n, iterable, key=None) 从 iterable 所定义的数据集中返回前 n 个最大元素组成的列表。如果提供了 key 则其应指定一个单参数的函数，用于从 iterable 的每个元素中提取比较键 (例如 key=str.lower)。等价于: sorted(iterable, key=key, reverse=True)[:n]。
heapq.nsmallest(n, iterable, key=None) 从 iterable 所定义的数据集中返回前 n 个最小元素组成的列表。如果提供了 key 则其应指定一个单参数的函数，用于从 iterable 的每个元素中提取比较键 (例如 key=str.lower)。等价于: sorted(iterable, key=key)[:n]。

常用方法示例

In [1]: import heapq ,random

In [2]: li = list(random.sample(range(100),6))

In [3]: li
Out[3]: [20, 98, 22, 96, 59, 6]

In [4]:  #nlargest
In [5]: heapq.nlargest(4, li)
Out[5]: [98, 96, 59, 22]

In [6]:  #nsmallest
In [7]:  heapq.nsmallest(4, li)
Out[7]: [6, 20, 22, 59]

In [8]: li
Out[8]: [20, 98, 22, 96, 59, 6]

In [9]: #heapify
In [10]: heapq.heapify(li)

In [11]: li
Out[11]: [6, 59, 20, 96, 98, 22]

In [12]:  # heappush & heappop
In [13]: heapq.heappush(li, 55)

In [14]: li
Out[14]: [6, 59, 20, 96, 98, 22, 55]

In [15]:  heapq.heappop(li)
Out[15]: 6

In [16]: li
Out[16]: [20, 59, 22, 96, 98, 55]

In [17]:

In [17]: # heappushpop & heapreplace
In [18]:  heapq.heappushpop(li, 40)
Out[18]: 20

In [19]: li
Out[19]: [22, 59, 40, 96, 98, 55]

In [20]: heapq.heapreplace(li, 2)
Out[20]: 22

In [21]: li
Out[21]: [2, 59, 40, 96, 98, 55]

堆排序示例

heapq 模块中有几种方法进行排序：

方法一：

def heap_sort(iterable):
    heap = []
    for i in iterable:
        heapq.heappush(heap, i)

    return [heapq.heappop(heap) for j in range(len(heap))]


if __name__ == "__main__":
    li = [30, 40, 60, 10, 20, 50]
    print(heap_sort(li))

方法二（使用 nlargest 或 nsmallest ）：

li = [30,40,60,10,20,50]
#nlargest
n = len(li)
print ("nlargest:",heapq.nlargest(n, li))
#nsmallest
print ("nsmallest:", heapq.nsmallest(n, li))

方法三（使用 heapify ）：

def heapsort(list):
    heapq.heapify(list)
    heap = []

    while(list):
        heap.append(heapq.heappop(list))
        
    li[:] = heap
    print (li)
        
if __name__ == "__main__":
    li = [30,40,60,10,20,50]
    heapsort(li)