主成分分析（PCA）原理

• PCA的推导:基于最小投影距离
• PCA的推导:基于最大投影方差
• PCA算法流程
• PCA计算过程
• python 代码
• 参考

主成分分析（Principal components analysis，以下简称PCA）是最重要的降维方法之一。在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。

PCA的推导:基于最小投影距离

即样本点到这个超平面的距离足够近。

假设m个n维数据 \((x^{(1)}, x^{(2)},...,x^{(m)})\) 都已经进行了中心化，即 \(\sum\limits_{i=1}^{m}x^{(i)}=0\) 。经过投影变换后得到的新坐标系为 \(\{w_1,w_2,...,w_n\}\) 其中$w$ 是标准正交基，即 ll\(w\)ll\(_2=1, w_i^Tw_j=0\) 。

如果我们将数据从 $n$ 维降到 $n’$ 维，即丢弃旧坐标系中的部分坐标，则新的坐标系为 \(\{w_1,w_2,...,w_{n'}\}\) ,样本点 $x^{(i)}$ 在 $n’$ 维坐标系中的投影为：$z^{(i)} = (z_1^{(i)}, z_2^{(i)},…,z_{n’}^{(i)})^T$ .其中，$z_j^{(i)} = w_j^Tx^{(i)}$ 是 $x^{(i)}$ 在低维坐标系里第j维的坐标。

如果我们用 $z^{(i)}$ 来恢复原始数据 $z^{(i)}$ ,则得到的恢复数据 $\overline{x}^{(i)} = \sum\limits_{j=1}^{n’}z_j^{(i)}w_j = Wz^{(i)}$ ,其中，W为标准正交基组成的矩阵。

现在我们考虑整个样本集，我们希望所有的样本到这个超平面的距离足够近，即最小化下式：

将这个式子进行整理，可以得到: \(\begin{align}\sum\limits_{i=1}^{m}||\overline{x}^{(i)} - x^{(i)}||_2^2 & = \sum\limits_{i=1}^{m}|| Wz^{(i)} - x^{(i)}||_2^2 \\& = \sum\limits_{i=1}^{m}(Wz^{(i)})^T(Wz^{(i)}) - 2\sum\limits_{i=1}^{m}(Wz^{(i)})^Tx^{(i)} + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = \sum\limits_{i=1}^{m}z^{(i)T}z^{(i)} - 2\sum\limits_{i=1}^{m}z^{(i)T}W^Tx^{(i)} +\sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = \sum\limits_{i=1}^{m}z^{(i)T}z^{(i)} - 2\sum\limits_{i=1}^{m}z^{(i)T}z^{(i)}+\sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = - \sum\limits_{i=1}^{m}z^{(i)T}z^{(i)} + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = -tr( W^T（\sum\limits_{i=1}^{m}x^{(i)}x^{(i)T})W) + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \\& = -tr( W^TXX^TW) + \sum\limits_{i=1}^{m} x^{(i)T}x^{(i)} \end{align}\)

　其中第（1）步用到了$\overline{x}^{(i)}=Wz^{(i)}$ ,第二步用到了平方和展开，第（3）步用到了矩阵转置公式 $(AB)^T =B^TA^T$ 和 $W^TW=I$ ,第（4）步用到了 $z^{(i)}=W^Tx^{(i)}$，第（5）步合并同类项，第（6）步用到了 $z^{(i)}=W^Tx^{(i)}$ 和矩阵的迹,第7步将代数和表达为矩阵形式。(每一行表示一步)

注意到 $\sum\limits_{i=1}^{m}x^{(i)}x^{(i)T}$ 是数据集的协方差矩阵，W的每一个向量 $w_j$是标准正交基。而 $\sum\limits_{i=1}^{m} x^{(i)T}x^{(i)}$

是一个常量。最小化上式等价于：

这个最小化不难，直接观察也可以发现最小值对应的W由协方差矩阵$XX^T$ 最大的 $n’$ 个特征值对应的特征向量组成。当然用数学推导也很容易。利用拉格朗日函数可以得到：

对W求导有 $-XX^TW+\lambda W=0$ 整理下即为：

这样可以更清楚的看出，W为 $XX^T$ 的 $n’$ 个特征向量组成的矩阵，而$λ$ 为$XX^T$ 的若干特征值组成的矩阵，特征值在主对角线上，其余位置为0。当我们将数据集从n维降到n’维时，需要找到最大的n’个特征值对应的特征向量。这 $n’$ 个特征向量组成的矩阵 $W$ 即为我们需要的矩阵。对于原始数据集，我们只需要用$z^{(i)}=W^Tx^{(i)}$ ,就可以把原始数据集降维到最小投影距离的n’维数据集。

PCA的推导:基于最大投影方差

假设m个n维数据 $ (x^{(1)}, x^{(2)},…,x^{(m)})$ 都已经进行了中心化，即$ \sum\limits_{i=1}^{m}x^{(i)}=0$ 。经过投影变换后得到的新坐标系为${w_1,w_2,…,w_n}$ ,其中$w$ 是标准正交基，即 ll\(w\) ll$_2=1, w_i^Tw_j=0$

如果我们将数据从$n$ 维降到 $n’$ 维，即丢弃新坐标系中的部分坐标，则新的坐标系为 ${w_1,w_2,…,w_{n’}}$ , 样本点$x^{(i)}$ 在n’维坐标系中的投影为：$z^{(i)} = (z_1^{(i)}, z_2^{(i)},…,z_{n’}^{(i)})^T$ .其中，$z_j^{(i)} = w_j^Tx^{(i)}$ 是$x^{(i)}$ 在低维坐标系里第j维的坐标。

对于任意一个样本$x^{(i)}$，在新的坐标系中的投影为$W^Tx^{(i)}$ ,在新坐标系中的投影方差为$W^Tx^{(i)}x^{(i)T}W$，要使所有的样本的投影方差和最大，也就是最大化 $\sum\limits_{i=1}^{m}W^Tx^{(i)}x^{(i)T}W$ 的迹,即：

观察上面的基于最小投影距离的优化目标，可以发现完全一样，只是一个是加负号的最小化，一个是最大化。

利用拉格朗日函数可以得到

对$W$ 求导有$XX^TW+\lambda W=0$ , 整理下即为：

和上面一样可以看出，$W$ 为$XX^T$ 的$n’$ 个特征向量组成的矩阵，而$−λ$为$XX^T$ 的若干特征值组成的矩阵，特征值在主对角线上，其余位置为0。当我们将数据集从$n$ 维降到$n’$ 维时，需要找到最大的$n’$ 个特征值对应的特征向量。这$n’$ 个特征向量组成的矩阵$W$ 即为我们需要的矩阵。对于原始数据集，我们只需要用$z^{(i)}=W^Tx^{(i)}$ ,就可以把原始数据集降维到最小投影距离的n’维数据集。

PCA算法流程

可以看出，求样本$x^{(i)}$ 的 $n’$ 维的主成分其实就是求样本集的协方差矩阵$XX^T$ 的前 $n’$ 个特征值对应特征向量矩阵 $W$ ，然后对于每个样本$x^{(i)}$ , 做如下变换$z^{(i)}=W^Tx^{(i)}$ ，即达到降维的PCA目的。

下面我们看看具体的算法流程。

输入：n 维样本集$D=(x^{(1)}, x^{(2)},…,x^{(m)})$ ，要降维到的维数 n’.

输出：降维后的样本集 D′

1) 对所有的样本进行中心化： $x^{(i)} = x^{(i)} - \frac{1}{m}\sum\limits_{j=1}^{m} x^{(j)}$

2) 计算样本的协方差矩阵 $XX^T$

3) 对矩阵$XX^T$ 进行特征值分解

4）取出最大的n’个特征值对应的特征向量 $(w_1,w_2,…,w_{n’})$ , 将所有的特征向量标准化后，组成特征向量矩阵W。

5）对样本集中的每一个样本 $x^{(i)}$ , 转化为新的样本 $z^{(i)}=W^Tx^{(i)}$

6) 得到输出样本集 $D’ =(z^{(1)}, z^{(2)},…,z^{(m)})$

有时候，我们不指定降维后的n’的值，而是换种方式，指定一个降维到的主成分比重阈值t。这个阈值t在（0,1]之间。假如我们的n个特征值为 $ \lambda_1 \geq \lambda_2 \geq … \geq \lambda_n$ , 则n’可以通过下式得到:

方差贡献率： 第 $k$ 主成分 $y_k$ 的方差贡献率定义为$y_k$ 的方差与所有方差之和的比：

累计方差贡献率： $k$ 个主成分$y_1, y_2, …,y_k$ 的累计方差贡献率定义为 $k$ 个方差之和与所有方差之和的比：

PCA计算过程

假设我们得到的2维数据如下：

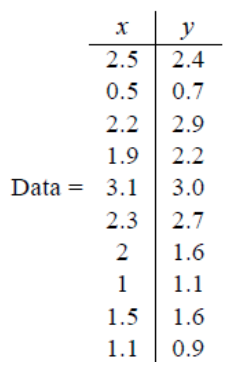
行代表了样例，列代表特征，这里有10个样例，每个样例两个特征。可以这样认为，有10篇文档，x是10篇文档中“learn”出现的TF-IDF，y是10篇文档中“study”出现的TF-IDF。也可以认为有10辆汽车，x是千米/小时的速度，y是英里/小时的速度，等等。

第一步分别求x和y的平均值，然后对于所有的样例，都减去对应的均值。这里x的均值是1.81，y的均值是1.91，那么一个样例减去均值后即为（0.69,0.49），得到

第二步，求特征协方差矩阵，如果数据是3维，那么协方差矩阵是

这里只有x和y，求解得

对角线上分别是x和y的方差，非对角线上是协方差。协方差大于0表示x和y若有一个增，另一个也增；小于0表示一个增，一个减；协方差为0时，两者独立。协方差绝对值越大，两者对彼此的影响越大，反之越小。

第三步，求协方差的特征值和特征向量，得到

上面是两个特征值，下面是对应的特征向量，特征值0.0490833989对应特征向量为\((-0.735178656,0.677873399)^{T}\)，这里的特征向量都归一化为单位向量。

第四步，将特征值按照从大到小的顺序排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。

这里特征值只有两个，我们选择其中最大的那个，这里是1.28402771，对应的特征向量是\((-0.677873399,-0.735178656)^{T}\)

第五步，将样本点投影到选取的特征向量上。假设样例数为m，特征数为n，减去均值后的样本矩阵为$DataAdjust(mn)$ ，协方差矩阵是$nn$ ，选取的k个特征向量组成的矩阵为$EigenVectors(n*k)$ 。那么投影后的数据FinalData为:

这里是:

得到结果是:

这样，就将原始样例的n维特征变成了k维，这k维就是原始特征在k维上的投影。

上面的数据可以认为是learn和study特征融合为一个新的特征叫做LS特征，该特征基本上代表了这两个特征。

python 代码

源码

参考

1. 主成分分析（PCA）原理总结
2. 主成分分析（Principal components analysis）-最大方差解释
3. PCA主成分分析Python实现
4. scikit-learn：降维算法PCA和SVD