感知机原理

• 1. 感知机模型
• 2. 感知机模型损失函数
• 3. 感知机模型损失函数的优化方法
• 3. 感知机模型的算法
• 4. 感知机模型的算法对偶形式
• 5. python 代码
• 参考

感知机可以说是最古老的分类方法之一了，在1957年就已经提出。今天看来它的分类模型在大多数时候泛化能力不强，但是它的原理却值得好好研究。因为研究透了感知机模型，学习支持向量机的话会降低不少难度。同时如果研究透了感知机模型，再学习神经网络，深度学习，也是一个很好的起点。

1. 感知机模型

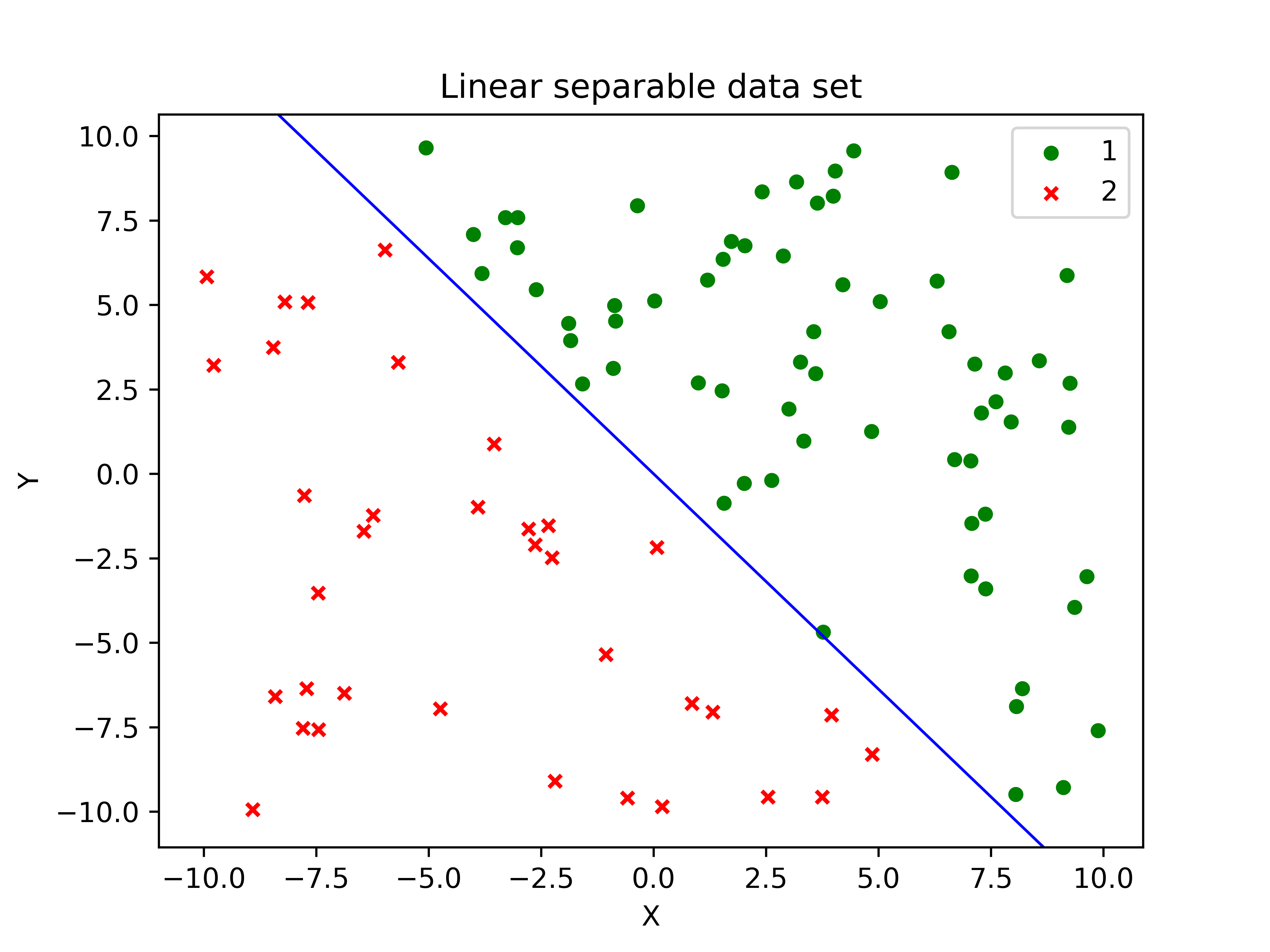
感知机的思想很简单，比如我们在一个平台上有很多的男孩女孩，感知机的模型就是尝试找到一条直线，能够把所有的男孩和女孩隔离开。放到三维空间或者更高维的空间，感知机的模型就是尝试找到一个超平面，能够把所有的二元类别隔离开。当然你会问，如果我们找不到这么一条直线的话怎么办？找不到的话那就意味着类别线性不可分，也就意味着感知机模型不适合你的数据的分类。使用感知机一个最大的前提，就是数据是线性可分的。这严重限制了感知机的使用场景。它的分类竞争对手在面对不可分的情况时，比如支持向量机可以通过核技巧来让数据在高维可分，神经网络可以通过激活函数和增加隐藏层来让数据可分。

感知机（perceptron）是二分类的线性分类模型，属于监督学习算法。

用数学的语言来说，如果我们有m个样本，每个样本对应于n维特征和一个二元类别输出，如下：

我们的目标是找到这样一个超平面，即：

让其中一种类别的样本都满足 $\theta_0 + \theta_{1}x_1 + … + \theta_{n}x_{n} > 0$ , 让另一种类别的样本都满足

$\theta_0 + \theta_{1}x_1 + … + \theta_{n}x_{n} < 0$ , 从而得到线性可分。如果数据线性可分，这样的超平面一般都不是唯一的，也就是说感知机模型可以有多个解。

为了简化这个超平面的写法，我们增加一个特征 $x_0 = 1$ ，这样超平面为 $\sum\limits_{i=0}^{n}\theta_{i}x_{i} = 0$ 进一步用向量来表示为：$\theta \bullet x = 0$ , 其中 $θ$ 为 $(n+1)\times1$ 的向量，$x$ 为 $(n+1)\times 1$ 的向量, ∙∙为内积，后面我们都用向量来表示超平面。

而感知机的模型可以定义为：$y = sign(\theta \bullet x)$ 其中：

2. 感知机模型损失函数

为了后面便于定义损失函数，我们将满足 $\theta \bullet x > 0$ 的样本类别输出值取为1，满足 $\theta \bullet x < 0$ 的样本类别输出值取为-1， 这样取y的值有一个好处，就是方便定义损失函数。因为正确分类的样本满足 $y\theta \bullet x > 0$ ，而错误分类的样本满足 $y\theta \bullet x < 0$ , 我们损失函数的优化目标，就是期望使误分类的所有样本，到超平面的距离之和最小。

由于 $y\theta \bullet x < 0$ ，所以对于每一个误分类的样本 $i $ ，到超平面的距离是

其中 $ ||\theta||_2$ 为L2范数。

我们假设所有误分类的点的集合为M，则所有误分类的样本到超平面的距离之和为：

这样我们就得到了初步的感知机模型的损失函数。

我们研究可以发现，分子和分母都含有 $θ$ ,当分子的 $θ$ 扩大 N 倍时，分母的 L2范数也会扩大N倍。也就是说，分子和分母有固定的倍数关系。那么我们可以固定分子或者分母为1，然后求另一个即分子自己或者分母的倒数的最小化作为损失函数，这样可以简化我们的损失函数。在感知机模型中，我们采用的是保留分子，即最终感知机模型的损失函数简化为：

3. 感知机模型损失函数的优化方法

感知机的损失函数：$J(\theta) = - \sum\limits_{x_i \in M}y^{(i)}\theta \bullet x^{(i)}$ , 其中M是所有误分类的点的集合。这个损失函数可以用梯度下降法或者拟牛顿法来解决，常用的是梯度下降法。但是用普通的基于所有样本的梯度和的均值的批量梯度下降法（BGD）是行不通的，原因在于我们的损失函数里面有限定，只有误分类的M集合里面的样本才能参与损失函数的优化。所以我们不能用最普通的批量梯度下降,只能采用随机梯度下降（SGD）或者小批量梯度下降（MBGD）。如果对这几种梯度下降法的区别不了解，可以参考另一篇文章梯度下降（Gradient Descent）小结。

感知机模型选择的是采用随机梯度下降，这意味着我们每次仅仅需要使用一个误分类的点来更新梯度。

损失函数基于 $θ$ 向量的的偏导数为：

$θ$ 的梯度下降迭代公式应该为：

由于我们采用随机梯度下降，所以每次仅仅采用一个误分类的样本来计算梯度，假设采用第 $i$ 个样本来更新梯度，则简化后的 $θ$ 向量的梯度下降迭代公式为：

其中 $α$ 为步长，$y^{(i)}$ 为样本输出 1 或者 -1，$x^{(i)}$ 为 $(n+1)\times 1$ 的向量。

3. 感知机模型的算法

算法的输入为 m 个样本，每个样本对应于 n 维特征和一个二元类别输出1或者-1，如下：

输出为分离超平面的模型系数 $θ$ 向量

算法的执行步骤如下：

1) 定义所有 $x_0$ 为1。选择 $x_0$ 向量的初值和 步长 $α$ 的初值。可以将 $x_0$ 向量置为 0 向量，步长设置为1。要注意的是，由于感知机的解不唯一，使用的这两个初值会影响 $x_0$ 向量的最终迭代结果。

2) 在训练集里面选择一个误分类的点 $(x_1^{(i)}, x_2^{(i)}, …x_n^{(i)}, y_i)$ , 用向量表示即 $(x^{(i)}, y^{(i)})$ , 这个点应该满足：$y^{(i)}\theta \bullet x^{(i)} \leq 0$

3) 对 $θ$ 向量进行一次随机梯度下降的迭代：$\theta = \theta + \alpha y^{(i)}x^{(i)}$

4）检查训练集里是否还有误分类的点，如果没有，算法结束，此时的 $θ$ 向量即为最终结果。如果有，继续第2步。

4. 感知机模型的算法对偶形式

　上一节的感知机模型的算法形式我们一般称为感知机模型的算法原始形式。对偶形式是对算法执行速度的优化。

通过上一节感知机模型的算法原始形式 $\theta = \theta + \alpha y^{(i)}x^{(i)}$ 可以看出，我们每次梯度的迭代都是选择的一个样本来更新 $θ$ 向量。最终经过若干次的迭代得到最终的结果。对于从来都没有误分类过的样本，他被选择参与 $ θ$ 迭代的次数是 0，对于被多次误分类而更新的样本 $j$，它参与 $θ$ 迭代的次数我们设置为 $m_j$ 。如果令 $θ$ 向量初始值为 0 向量， 这样我们的 $θ$ 向量的表达式可以写为：

其中 $m_j$ 为样本 $(x^{(j)}, y^{(j)})$ 在随机梯度下降到当前的这一步之前因误分类而更新的次数。

每一个样本 $(x^{(j)}, y^{(j)})$ 的 $m_j$ 的初始值为0，每当此样本在某一次梯度下降迭代中因误分类而更新时，$m_j$ 的值加 1。

由于步长 $α$ 为常量，我们令 $\beta_j = \alpha m_j$ ,这样 $θ$ 向量的表达式为:

\(\theta = \sum\limits_{j=1}^{m}\beta_j y^{(j)}x^{(j)}\) 在每一步判断误分类条件的地方，我们用 $y^{(i)}\theta \bullet x^{(i)} < 0$ 的变种 $y^{(i)}\sum\limits_{j=1}^{m}\beta_j y^{(j)}x^{(j)}\bullet x^{(i)} < 0$ 来判断误分类。

注意到这个判断误分类的形式里面是计算两个样本 $x^{(i)}和x^{(j)}$ 的内积，而且这个内积计算的结果在下面的迭代次数中可以重用。如果我们事先用矩阵运算计算出所有的样本之间的内积，那么在算法运行时， 仅仅一次的矩阵内积运算比多次的循环计算省时。 计算量最大的判断误分类这儿就省下了很多的时间，，这也是对偶形式的感知机模型比原始形式优的原因。

样本的内积矩阵称为Gram矩阵，它是一个对称矩阵，记为 $G = [x^{(i)} \bullet x^{(j)} ]$

这里给出感知机模型的算法对偶形式的内容。

算法的输入为 m 个样本，每个样本对应于 n 维特征和一个二元类别输出 1 或者 -1，如下：

输出为分离超平面的模型系数 $θ$ 向量

算法的执行步骤如下：

1) 定义所有 $x_0$ 为 1，步长 $α$ 初值，设置 $β$ 的初值 0。可以将 $α$ 设置为 1。要注意的是，由于感知机的解不唯一，使用的步长初值会影响 $θ$ 向量的最终迭代结果。

2) 计算所有样本内积形成的 Gram 矩阵 G。

2) 在训练集里面选择一个误分类的点 $(x^{(i)}, y^{(i)})$ ，这个点应该满足：$y^{(i)}\sum\limits_{j=1}^{m}\beta_j y^{(j)}x^{(j)}\bullet x^{(i)} \leq 0$ , 在检查是否满足时可以通过查询 Gram 矩阵的 $g_{ij}$ 的值来快速计算是否小于0。

3) 对 $β$ 向量的第 $i$ 个分量进行一次更新：$\beta_i= \beta_i+ \alpha$

4）检查训练集里是否还有误分类的点，如果没有，算法结束，此时的 $θ$ 向量最终结果为下式。如果有，继续第2步。

其中 $\beta_j$ 为 $β$ 向量的第j个分量。

5. python 代码

一般形式：

核心算法：

    separated = False
    i = 0
    alpha = 0.5
    while not separated and i < numLines:
        if dataSet[i][-1] * np.sum(w * dataSet[i, 0:-1]) <= 0:  # 如果分类错误
            w = w + alpha * dataSet[i][-1] * dataSet[i, 0:-1]  # 更新权重向量
            separated = False  # 设置为未完全分开
            i = 0  # 重新开始遍历每个数据点
        else:
            i += 1  # 如果分类正确，检查下一个数据点

源码

参考

1. 感知机原理小结
2. 第2章 感知机
3. 感知机（Perceptron）及python实现