拉格朗日乘数法

1. 拉格朗日乘数法的基本思想
2. 求解不同约束条件问题的最优方法
参考

在求解优化问题或者多元不等式时，我们经常需要在某些约束条件（constraints）下求极值，而这些约束条件经常会使解答变得十分复杂，拉格朗日乘数法（Method of Lagrange Multipliers）能巧妙的解决这一问题。

1. 拉格朗日乘数法的基本思想

作为一种优化算法，拉格朗日乘子法主要用于解决约束优化问题，它的基本思想就是通过引入拉格朗日乘子来将含有n个变量和k个约束条件的约束优化问题转化为含有（n+k）个变量的无约束优化问题。拉格朗日乘子背后的数学意义是其为约束方程梯度线性组合中每个向量的系数。

如何将一个含有n个变量和k个约束条件的约束优化问题转化为含有（n+k）个变量的无约束优化问题？拉格朗日乘数法从数学意义入手，通过引入拉格朗日乘子建立极值条件，对n个变量分别求偏导对应了n个方程，然后加上k个约束条件（对应k个拉格朗日乘子）一起构成包含了（n+k）变量的（n+k）个方程的方程组问题，这样就能根据求方程组的方法对其进行求解。

约束条件分为两种，一种是等式约束；另一种是不等式约束。对于第一种等式约束的优化问题，可以直接利用拉格朗日乘子法去获得最优解；对于不等式约束的优化问题，可以转化未Karush–Kuhn–Tucker conditions（KKT条件）下去应用拉格朗日乘子法求解。也就是说都是应用拉格朗日乘数法求解。

解决的问题模型为约束优化问题：

min/max a function f(x,y,z), where x,y,z are not independent and g(x,y,z)=0.

即：

\[\begin{equation} \begin{aligned} &\min / \max \mathrm{f}(\mathrm{x}, \mathrm{y}, \mathrm{z})\\ &\text { s. t. }\quad g(x, y, z)=0 \end{aligned} \end{equation}\]

2. 求解不同约束条件问题的最优方法

1. 约束条件的集中形式

等式条件下的最优解：
\[\begin{equation} \begin{aligned} \min \quad &f(x, y) \\ \text {s.t.} \quad &h_{i}(x, y)=c,\quad i=1,2,3 \dots l \end{aligned} \end{equation}\]
不等式条件下的最优解：
\[\begin{equation} \begin{aligned} \min \quad&f(x)\\ s.t.\quad &h_{j}(x)=0, \quad j=1,2,3 \dots l\\ &g_{i}(x) \leq 0,\quad i=1,2,3 \dots l^{\prime} \end{aligned} \end{equation}\]

2. 等式条件下求最优解

首先构建一个Lagrange multiplier：

\[\begin{equation} L(x, y, \lambda)=f(x, y)+\lambda \varphi(\boldsymbol{x}, \boldsymbol{y}) \end{equation}\]

将函数 $z=f(x, y)$ 在满足 $\varphi(x, y)=0$ 下的条件极值，可以转化为函数 $\boldsymbol{F}(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{\lambda})=\boldsymbol{f}(\boldsymbol{x}, \boldsymbol{y})+\lambda \varphi(\boldsymbol{x}, \boldsymbol{y})$ 的无条件极值问题。

(拉格朗日乘子求的解不一定是最优解，其实只是局部最优解，这里称作可行解，只有在凸函数中才能保证最优解)

可以画图来辅助思考：

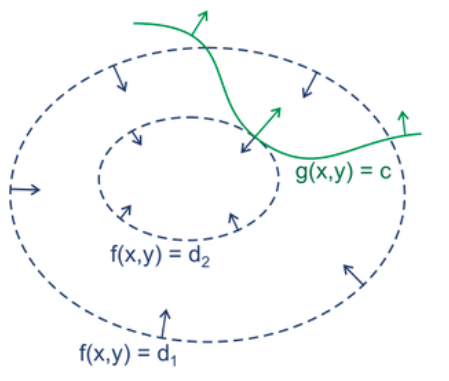
绿线标出的是约束 g(x,y)=c 的点的轨迹。蓝线是 f(x,y) 的等高线。箭头表示斜率，和等高线的法线平行。

目标函数和条件函数有三种情况：

1、相离

对于相离的情况，我们以前学过，两个函数有交点才说明是两个函数的解，所以相离明显不行。

2、相交

两个函数相交的才是两个函数的解，但是相交得到的一定不是最优值，因为相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部，使得新的等高线与目标函数的交点的值更大或者更小。

3、相切

图中，等高线与条件函数相切时候，只有一个交点，是可行解。

当等高线与条件函数在可行解处（相切时候）的梯度平行有下式：

\[\begin{equation} \nabla f(x)=-\lambda \nabla(g(x)-c) \end{equation}\]

对上式子移项后，可得到：

\[\begin{equation} \nabla L(x, y, \lambda)=\nabla f(x)+\lambda \nabla(g(x)-c)=0 \end{equation}\]

该式子恰好与令Lagrange multiplier的导数为零是式子相同。

从图上可以直观地看到在最优解处，f 和 g 的斜率平行。

\[\begin{equation} \nabla[\mathrm{f}(\mathrm{x}, \mathrm{y})+\lambda(\mathrm{g}(\mathrm{x}, \mathrm{y})-1)]=0, \quad \lambda \neq 0 \end{equation}\]

一旦求出 $λ$ 的值，将其套入下式，易求在无约束极值和极值所对应的点。

\[\begin{equation} \mathrm{F}(\mathrm{x}, \mathrm{y})=\mathrm{f}(\mathrm{x}, \mathrm{y})+\lambda(\mathrm{g}(\mathrm{x}, \mathrm{y})-\mathrm{c}) \end{equation}\]

新方程F(x,y)在达到极值时与 f(x,y) 相等，因为 F(x,y) 达到极值时g(x,y)−c总等于零。

上述式子取得极小值时其导数为0，即 $\nabla \mathrm{f}(\mathrm{x})+\nabla \sum \lambda_{\mathrm{i}} \mathrm{g}_{\mathrm{i}}(\mathrm{x})=0$ ，也就是说f(x)和g(x)的梯度共线。

实例

求双曲线xy=3上离原点最近的点。

首先，我们根据问题的描述来提炼出问题对应的数学模型，即：$min f(x,y)=x^2+y^2$（两点之间的欧氏距离应该还要进行开方，但是这并不影响最终的结果，所以进行了简化，去掉了平方）

s.t. xy=3.

即：

\[\begin{equation} \begin{array}{cl} {\min f(x, y)} & {=x^{2}+y^{2}} \\ {s . t .} & {x y=3} \end{array} \end{equation}\]

根据上式子可知是一个典型的约束优化问题，约束条件是等式，可以用拉格朗日乘子。

\[\begin{equation} L(x, y, \lambda)=x^{2}+y^{2}+\lambda(x y-3) \end{equation}\]

原来的条件约束问题，转化为无约束方程组问题。

\[\begin{equation} \begin{array}{r} {2 x+\lambda y=0} \\ {2 y+\lambda x=0} \\ {x y-3=0} \end{array} \end{equation}\] \[\begin{equation} \begin{aligned} & \text { 求得 } \lambda=\pm 2,{\text { 当 }}\lambda=2 \text { 时 } x=\sqrt{3}, y=\sqrt{3} ; {\text { 当 }} \lambda=-2, \quad x=-\sqrt{3}\\ &y=-\sqrt{3} \end{aligned} \end{equation}\]

3. 不等式条件下求最优解

上述都是等式条件约束的优化问题，但事实上，很多时候等式约束很难覆盖我们显示的问题，计算成本时候，通常说不能超过多少资金，不能超多多少时间，都是一个范围内，通常面对更多的是不等式条件约束的情况，面对这种情况，可以通过增加KKT条件后，通过拉格朗日乘子求解不等式约束的优化问题。

可以把目标函数和所有的约束条件写成一个式子：

\[\begin{equation} L(x, \lambda, \mu)=f(x)+\sum_{i=1}^{l^{\prime}} \lambda_{i} g_{i}(x)+\sum_{j=1}^{l} \mu_{j} h_{j}(x) \end{equation}\]

对于不等式条件的情况有两种：即可行解在 $g(x)<0$ 或者 $g(x)=0$ 区域内取得（如下图）

在 g(x) < 0 内，就是没有限制条件下的最优解，正好满足限制条件，换句话说约束函数不起作用 (如上图左侧) ，这种情况下直接最小化目标函数，找可行解 $x^*$ ,所以有：
\[\begin{equation} \nabla_{x^{*}} f\left(x^{*}\right)=0, \quad \lambda=0, \quad g\left(x^{*}\right)<0 \end{equation}\]
在 g(x) = 0 上，换句话说，就是没有限制条件下的最优解，不能满足限制条件，需要条件起作用，此时 $\lambda \neq 0$ ，因此可行解在 $g(x)=0$ 上，就变成等式条件约束的情况，经之前分析，可以证明可行解 $x^{*}$ 发生在 $\nabla f(x)=-\lambda \nabla g(x)$ ，即是说，存在一个 $\lambda $ 使得 $\nabla f(x^*)=-\lambda \nabla g(x^*)$ 为确定 $\lambda $ 范围，回看图一，梯度 $\nabla f(x)$ 方向与梯度 $ \nabla g(x)$ 的方相反且梯度平行，所以，若要使得 $\nabla f(x)=-\lambda \nabla g(x)$ ，则 $\lambda \gt 0$ ，所以有：

\[\begin{equation} g\left(x^{*}\right)=0, \quad \lambda>0 \end{equation}\]

把两个情况综合考虑得到：

\[\begin{equation} \begin{aligned} \lambda & \ge0 \\ \lambda g\left(x^{*}\right) &=0 \\ g\left(x^{*}\right) & \leq 0 \end{aligned} \end{equation}\]

以上就是KKT条件。

考虑不等式条件下求最优解时：

\[\begin{equation} \begin{aligned} \min &f(x)\\ s.t.\quad &h_{j}(x)=0,\quad j=1,2,3 \dots l\\ &g_{i}(x) \leq 0,\quad i=1,2,3 \dots l \end{aligned} \end{equation}\]

定义拉格朗日函数：

\[\begin{equation} L(x, \lambda, \mu)=f(x)+\sum_{i=1}^{l^{\prime}} \lambda_{i} g_{i}(x)+\sum_{j=1}^{l} \mu_{j} h_{j}(x) \end{equation}\]

其中 $\lambda_i $ 是 $g_{i}(x) \leq 0$ 的格朗日乘子， $\mu_{j} $ 是 $h_{j}(x)=0$ 的拉格朗日乘子。

经过之前的分析观察，得知加上不等式约束后可行解 $x$ 需要满足的就是以下的 KKT 条：

\[\begin{align} \nabla_{x} L(x, \lambda, \mu)&=0 \tag{1}\\ h_{j}(x)&=0, \quad j=1,2,3 \dots l\tag{2}\\ g_{i}(x) &\leq 0, \quad i=1,2,3 \dots l^{\prime}\tag{3}\\ \lambda_{i} &\ge 0, \quad i=1,2,3 \dots l^{\prime} \tag{4}\\ \lambda_{i} g_{i}(x)&=0, \quad i=1,2,3 \dots l^{\prime}\tag{5} \end{align}\]

KKT条件

①：拉格朗日取得可行解的必要条件
②：初始的约束条件
③：初始的约束条件
④：不等式条件的两种情况下得出 $\lambda $ 满足的条件($λ≥0$ , 这是不等式约束与等式约束最优化问题拉格朗日乘数法的一个重要区别。)
⑤：不等式条件的两种情况下，无论是哪一种情况，都满足 $\lambda_{i}g_{i}(x) = 0$ ，称作松弛互补条件