- 1. 线性分类SVM面临的问题
- 2. 线性分类SVM的软间隔最大化
- 3. 线性分类SVM的软间隔最大化目标函数的优化
- 4. 软间隔最大化时的支持向量
- 5. 软间隔最大化的线性可分SVM的算法过程
- 参考
在支持向量机原理(一) 线性支持向量机中,我们对线性可分SVM的模型和损失函数优化做了总结。有时候不能线性可分的原因是线性数据集里面多了少量的异常点,由于这些异常点导致了数据集不能线性可分,本篇就对线性支持向量机如何处理这些异常点的原理方法做一个总结。
1. 线性分类SVM面临的问题
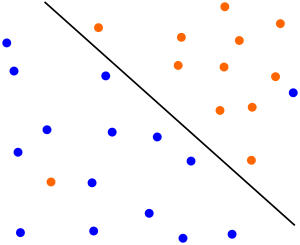
有时候本来数据的确是可分的,也就是说可以用 线性分类SVM的学习方法来求解,但是却因为混入了异常点,导致不能线性可分,比如下图,本来数据是可以按下面的实线来做超平面分离的,可以由于一个橙色和一个蓝色的异常点导致我们没法按照上一篇线性支持向量机中的方法来分类。
另外一种情况没有这么糟糕到不可分,但是会严重影响我们模型的泛化预测效果,比如下图,本来如果我们不考虑异常点,SVM的超平面应该是下图中的红色线所示,但是由于有一个蓝色的异常点,导致我们学习到的超平面是下图中的粗虚线所示,这样会严重影响我们的分类模型预测效果。

如何解决这些问题呢?SVM引入了软间隔最大化的方法来解决。
2. 线性分类SVM的软间隔最大化
所谓的软间隔,是相对于硬间隔说的,我们可以认为上一篇线性分类SVM的学习方法属于硬间隔最大化。
回顾下硬间隔最大化的条件:
\[\begin{equation} \begin{aligned} &\min \frac{1}{2}\|w\|_{2}^{2} \\\text { s.t }\quad &y_{i}\left(w^{T} x_{i}+b\right) \geq 1\qquad(i=1,2, \dots m) \end{aligned} \end{equation}\]SVM对训练集里面的每个样本 $(x_i,y_i)$ 引入了一个松弛变量 $\xi_i \geq 0$ ,使函数间隔加上松弛变量大于等于1,也就是说:
\[y_i(w\bullet x_i +b) \geq 1- \xi_i\]对比硬间隔最大化,可以看到我们对样本到超平面的函数距离的要求放松了,之前是一定要大于等于1,现在只需要加上一个大于等于0的松弛变量能大于等于1就可以了。当然,松弛变量不能白加,这是有成本的,每一个松弛变量 $\xi_i $ , 对应了一个代价 $\xi_i $ , 这个就得到了我们的软间隔最大化的 SVM 学习条件如下:
\[min\;\; \frac{1}{2}||w||_2^2 +C\sum\limits_{i=1}^{m}\xi_i\] \[s.t. \;\; y_i(w^Tx_i + b) \geq 1 - \xi_i \;\;(i =1,2,...m)\] \[\xi_i \geq 0 \;\;(i =1,2,...m)\]这里, $C>0$ 为惩罚参数,可以理解为我们一般回归和分类问题正则化时候的参数。$C$ 越大,对误分类的惩罚越大,$C$ 越小,对误分类的惩罚越小。
也就是说,我们希望 $\frac{1}{2}| |w||_2^2$ 尽量小,误分类的点尽可能的少。C 是协调两者关系的正则化惩罚系数。在实际应用中,需要调参来选择。
这个目标函数的优化和上一篇的线性可分 SVM 的优化方式类似,我们下面就来看看怎么对线性分类SVM的软间隔最大化来进行学习优化。
3. 线性分类SVM的软间隔最大化目标函数的优化
和线性可分 SVM 的优化方式类似,我们首先将软间隔最大化的约束问题用拉格朗日函数转化为无约束问题如下:
\[L(w,b,\xi,\alpha,\mu) = \frac{1}{2}||w||_2^2 +C\sum\limits_{i=1}^{m}\xi_i - \sum\limits_{i=1}^{m}\alpha_i[y_i(w^Tx_i + b) - 1 + \xi_i] - \sum\limits_{i=1}^{m}\mu_i\xi_i\]其中 $\mu_i \geq 0, \alpha_i \geq 0$ ,均为拉格朗日系数。
也就是说,我们现在要优化的目标函数是:
\[\underbrace{min}_{w,b,\xi}\; \underbrace{max}_{\alpha_i \geq 0, \mu_i \geq 0,} L(w,b,\alpha, \xi,\mu)\]这个优化目标也满足 KKT 条件,也就是说,我们可以通过拉格朗日对偶将我们的优化问题转化为等价的对偶问题来求解如下:
\[\underbrace{max}_{\alpha_i \geq 0, \mu_i \geq 0,} \; \underbrace{min}_{w,b,\xi}\; L(w,b,\alpha, \xi,\mu)\]我们可以先求优化函数对于 $w, b, \xi$ 的极小值, 接着再求拉格朗日乘子 $\alpha$ 和 $\mu$ 的极大值。
首先我们来求优化函数对于 $w, b, \xi$ 的极小值,这个可以通过求偏导数求得:
\[\frac{\partial L}{\partial w} = 0 \;\Rightarrow w = \sum\limits_{i=1}^{m}\alpha_iy_ix_i\] \[\frac{\partial L}{\partial b} = 0 \;\Rightarrow \sum\limits_{i=1}^{m}\alpha_iy_i = 0\] \[\frac{\partial L}{\partial \xi} = 0 \;\Rightarrow C- \alpha_i - \mu_i = 0\]好了,我们可以利用上面的三个式子去消除 $w$ 和 $b$ 了。
\[\begin{align} L(w,b,\xi,\alpha,\mu) & = \frac{1}{2}||w||_2^2 +C\sum\limits_{i=1}^{m}\xi_i - \sum\limits_{i=1}^{m}\alpha_i[y_i(w^Tx_i + b) - 1 + \xi_i] - \sum\limits_{i=1}^{m}\mu_i\xi_i \tag{1} \\&= \frac{1}{2}||w||_2^2 - \sum\limits_{i=1}^{m}\alpha_i[y_i(w^Tx_i + b) - 1 + \xi_i] + \sum\limits_{i=1}^{m}\alpha_i\xi_i \tag{2}\\& = \frac{1}{2}||w||_2^2 - \sum\limits_{i=1}^{m}\alpha_i[y_i(w^Tx_i + b) - 1]\tag{3} \\& = \frac{1}{2}w^Tw-\sum\limits_{i=1}^{m}\alpha_iy_iw^Tx_i - \sum\limits_{i=1}^{m}\alpha_iy_ib + \sum\limits_{i=1}^{m}\alpha_i \tag{4}\\& = \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i -\sum\limits_{i=1}^{m}\alpha_iy_iw^Tx_i - \sum\limits_{i=1}^{m}\alpha_iy_ib + \sum\limits_{i=1}^{m}\alpha_i \tag{5}\\& = \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - \sum\limits_{i=1}^{m}\alpha_iy_ib + \sum\limits_{i=1}^{m}\alpha_i \tag{6} \\& = - \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - \sum\limits_{i=1}^{m}\alpha_iy_ib + \sum\limits_{i=1}^{m}\alpha_i \tag{7} \\& = - \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - b\sum\limits_{i=1}^{m}\alpha_iy_i + \sum\limits_{i=1}^{m}\alpha_i \tag{8} \\& = -\frac{1}{2}(\sum\limits_{i=1}^{m}\alpha_iy_ix_i)^T(\sum\limits_{i=1}^{m}\alpha_iy_ix_i) - b\sum\limits_{i=1}^{m}\alpha_iy_i + \sum\limits_{i=1}^{m}\alpha_i \tag{9} \\& = -\frac{1}{2}\sum\limits_{i=1}^{m}\alpha_iy_ix_i^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - b\sum\limits_{i=1}^{m}\alpha_iy_i + \sum\limits_{i=1}^{m}\alpha_i \tag{10} \\& = -\frac{1}{2}\sum\limits_{i=1}^{m}\alpha_iy_ix_i^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i + \sum\limits_{i=1}^{m}\alpha_i \tag{11} \\& = -\frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_iy_ix_i^T\alpha_jy_jx_j + \sum\limits_{i=1}^{m}\alpha_i \tag{12} \\& = \sum\limits_{i=1}^{m}\alpha_i - \frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j \tag{13} \end{align}\]其中 :
(1)式到(2)式用到了 $C- \alpha_i - \mu_i = 0$ .
(2)式到(3)式合并了同类项,
(3)式到(4)式用到了范数的定义 $||w||_2^2 =w^Tw$
(4)式到(5)式用到了上面的 $w = \sum\limits_{i=1}^{m}\alpha_iy_ix_i$
(5)式到(6)式把和样本无关的 $w^T$ 提前,
(6)式到(7)式合并了同类项,
(7)式到(8)式把和样本无关的 $b$ 提前,
(8)式到(9)式继续用到 $w = \sum\limits_{i=1}^{m}\alpha_iy_ix_i$
(9)式到(10)式用到了向量的转置。由于常量的转置是其本身,所有只有向量 $x_i$ 被转置,
(10)式到(11)式用到了上面的 $\sum\limits_{i=1}^{m}\alpha_iy_i = 0$
(11)式到(12)式使用了 $(a+b+c+…)(a+b+c+…)=aa+ab+ac+ba+bb+bc+…$ 的乘法运算法则,
(12) 式到 (13) 式仅仅是位置的调整。
仔细观察可以发现,这个式子和我们上一篇线性可分SVM的一样。唯一不一样的是约束条件。现在我们看看我们的优化目标的数学形式:
\[\underbrace{ max }_{\alpha} \sum\limits_{i=1}^{m}\alpha_i - \frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j\] \[s.t. \; \sum\limits_{i=1}^{m}\alpha_iy_i = 0\] \[C- \alpha_i - \mu_i = 0\] \[\alpha_i \geq 0 \;(i =1,2,...,m)\] \[\mu_i \geq 0 \;(i =1,2,...,m)\]对于 $C- \alpha_i - \mu_i = 0 , \alpha_i \geq 0 ,\mu_i \geq 0$ 这3个式子,我们可以消去 $\mu_i$ ,只留下 $\alpha_i$ ,也就是说 $0 \leq \alpha_i \leq C$ . 同时将优化目标函数变号,求极小值,如下:
\[\underbrace{ min }_{\alpha} \frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j - \sum\limits_{i=1}^{m}\alpha_i\] \[s.t. \; \sum\limits_{i=1}^{m}\alpha_iy_i = 0\] \[0 \leq \alpha_i \leq C\]这就是软间隔最大化时的线性可分SVM的优化目标形式,和上一篇的硬间隔最大化的线性可分SVM相比,我们仅仅是多了一个约束条件 $0 \leq \alpha_i \leq C$ , 我们依然可以通过SMO算法来求上式极小化时对应的 $α$ 向量就可以求出 $w$ 和 $b$ 了。
4. 软间隔最大化时的支持向量
在硬间隔最大化时,支持向量比较简单,就是满足 $y_i(w^Tx_i + b) -1 =0$ 就可以了。根据KKT条件中的对偶互补条件 $\alpha_{i}^{* }(y_i(w^Tx_i + b) - 1) = 0$ ,如果 $\alpha_{i}^{*}>0$ 则有 $y_i(w^Tx_i + b) =1$ 即点在支持向量上,否则如果 $\alpha_{i}^{ * }=0$ 则有 $y_i(w^Tx_i + b) \geq 1$ ,即样本在支持向量上或者已经被正确分类。
在软间隔最大化时,则稍微复杂一些,因为我们对每个样本 $(x_i,y_i)$ 引入了松弛变量 $\xi_i$ 。我们从下图来研究软间隔最大化时支持向量的情况,第 $i$ 个点到对应类别支持向量的距离为
$\frac{\xi_i}{||w||_2}$ 。
根据软间隔最大化时KKT条件中的对偶互补条件
$\alpha_{i}^{* }(y_i(w^Tx_i + b) - 1 + \xi_i^{* }) = 0$
我们有:
a) 如果 $\alpha = 0$ ,那么 $y_i(w^Tx_i + b) - 1 \geq 0$ ,即样本在间隔边界上或者已经被正确分类。如图中所有远离间隔边界的点。
b) 如果 $0 < \alpha < C$ ,那么 $\xi_i = 0 ,\;\; y_i(w^Tx_i + b) - 1 = 0$ ,即点在间隔边界上。
c) 如果 $\alpha = C$ ,说明这是一个可能比较异常的点,需要检查此时 $\xi_i$
i)如果 $0 \leq \xi_i \leq 1$ ,那么点被正确分类,但是却在超平面和自己类别的间隔边界之间。如图中的样本2和4.
ii)如果 $\xi_i =1$ ,那么点在分离超平面上,无法被正确分类。
iii)如果 $\xi_i > 1$ ,那么点在超平面的另一侧,也就是说,这个点不能被正常分类。如图中的样本1和3.

5. 软间隔最大化的线性可分SVM的算法过程
这里我们对软间隔最大化时的线性可分SVM的算法过程做一个总结。
输入是线性可分的m个样本 ${(x_1,y_1), (x_2,y_2), …, (x_m,y_m),}$ 其中x为n维特征向量。y为二元输出,值为1,或者-1.
输出是分离超平面的参数 $w^{*}和b^{*}$ 和分类决策函数。
算法过程如下:
1)选择一个惩罚系数 $C>0$ , 构造约束优化问题
\[\underbrace{ min }_{\alpha} \frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j - \sum\limits_{i=1}^{m}\alpha_i\] \[s.t. \; \sum\limits_{i=1}^{m}\alpha_iy_i = 0\] \[0 \leq \alpha_i \leq C\]2)用SMO算法求出上式最小时对应的 $\alpha$ 向量的值 $\alpha^{*}$ 向量.
3) 计算 $w^{*} = \sum\limits_{i=1}^{m}\alpha_i^{*}y_ix_i$
4) 找出所有的S个支持向量对应的样本 $(x_s,y_s)$ ,通过 $y_s(\sum\limits_{i=1}^{m}\alpha_iy_ix_i^Tx_s+b) = 1$ ,计算出每个支持向量 $(x_x, y_s)$ 对应的 $b_s^{*}$ ,计算出这些 $b_s^{*} = y_s - \sum\limits_{i=1}^{m}\alpha_iy_ix_i^Tx_s$ . 所有的 $b_s^{*}$ 对应的平均值即为最终的 $b^{*} = \frac{1}{S}\sum\limits_{i=1}^{S}b_s^{*} $
这样最终的分类超平面为:$w^{* } \bullet x + b^{\ *} = 0$ ,最终的分类决策函数为: $f(x) = sign(w^{* } \bullet x + b^{* })$