插值法主要用来做什么事:插值法就是利用已知的点建立合适的插值函数 $f(x)$ , 未知点 $x_i$ 由插值函数 $f(x)$ 可以求出函数值 $f(x_i)$ , 用求得的 $(x_i, f(x_i))$ 近似代替未知点。
对于平面上相异(无两点在一条直线上, 点是线性无关的 ,函数存在且唯一)的 $n$个点,我们必定可以找到一个 $n-1$ 次多项式 \(y=a_{0}+a_{1} x+a_{2} x^{2}+\ldots a_{n-1} x^{n-1}\) ,使这个多项式函数经过这些点。拉格朗日插值法和牛顿插值法所要做的就是求得这个多项式函数。只是求得多项式的方式有些不同,下面详细介绍。
拉格朗日插值法
\1. 已知 $n$ 个点的坐标 \(\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right),\left(x_{3}, y_{3}\right) \dots\left(x_{n}, y_{n}\right)\) 求得一个 $n-1$ 次多项式 过这些点。
\2. 假设 $n-1$ 次多项式为 \(y=a_{0}+a_{1} x+a_{2} x^{2}+\ldots a_{n-1} x^{n-1}\)
\3. 将 $n$ 个点代入多项式得:
\[\begin{equation} \begin{aligned} &y_{1}=a_{0}+a_{1} x_{1}+a_{2} x_{1}^{2}+\ldots a_{n-1} x_{1}^{n-1}\\ &y_{2}=a_{0}+a_{1} x_{2}+a_{2} x_{2}^{2}+\ldots a_{n-1} x_{2}^{n-1}\\ &......\\ &y_{n}=a_{0}+a_{1} x_{n}+a_{2} x_{n}^{2}+\ldots a_{n-1} x_{n}^{n-1} \end{aligned} \end{equation}\]\4. 易解出拉格朗日插值多项式为:
\[\begin{equation} \begin{aligned} L(x)&=y_{1} \frac{\left(x-x_{2}\right)\left(x-x_{3}\right) \ldots\left(x-x_{n}\right)}{\left(x_{1}-x_{2}\right)\left(x_{1}-x_{3}\right) \ldots\left(x_{1}-x_{n}\right)}\\ &+y_{2} \frac{\left(x-x_{1}\right)\left(x-x_{3}\right) \ldots\left(x-x_{n}\right)}{\left(x_{2}-x_{1}\right)\left(x_{2}-x_{3}\right) \ldots\left(x_{2}-x_{n}\right)}+\\ &\ldots \\&+y_{n} \frac{\left(x-x_{1}\right)\left(x-x_{2}\right) \ldots\left(x-x_{n-1}\right)}{\left(x_{n}-x_{1}\right)\left(x_{n}-x_{2}\right) \ldots\left(x_{n}-x_{n-1}\right)} \end{aligned} \end{equation}\]\5. 上式也可以写为:
\[\begin{equation} L(x)=\sum_{i=1}^{n} y_{i} \prod_{j=1, j \neq i}^{n} \frac{x-x_{j}}{x_{i}-x_{j}} \end{equation}\]拉格朗日插值公式在理论分析理解上很容易理解,但是若插值节点发生改变时,插值公式随之就要重新计算生成,在实际计算中会占用大量的计算量。e.g. 现在有n个节点生成的插值公式,这里第 n+1 个节点也要加入进去,若使用拉格朗日插值法,之前的n个节点生成的插值公式则要完全调整废弃,重新生成含 n+1 个节点插值公式,这样就带来很大的计算量。正常的想法是,当一个节点要加入,我们只需在原来的插值公式上稍加修改就可以得到新的插值公式,牛顿法的出现正是克服这个问题,当插值节点发生增加,新的插值公式基于原来的公式很容易就得到。
牛顿插值法
差商:
设函数 $f(x)$ , 已知其 $n$ 个插值节点为 \(\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right),\left(x_{3}, y_{3}\right) \ldots\left(x_{n}, y_{n}\right)\) ,定义:、
-
一阶差商
\[\begin{equation} f\left[x_{i}, x_{j}\right]=\frac{f\left(x_{i}\right)-f\left(x_{j}\right)}{x_{i}-x_{j}}, i \neq j \end{equation}\] -
二阶差商
\[\begin{equation} f\left[x_{i}, x_{j}, x_{k}\right]=\frac{f[i, j]-f[j, k]}{x_{i}-x_{k}}, i \neq j \neq k \end{equation}\] -
n 阶差商
\[\begin{equation} f\left[x_{0}, x_{1}, ..., x_{n}\right]=\frac{f\left[x_{0}, x_{1}, ..., x_{n-1}\right]-f\left[x_{1}, x_{2}, ..., x_{n}\right]}{x_{0}-x_{n}} \end{equation}\]
以此类推,我们得到牛顿插值法为:
计算通过下面这个示意图进行,就会很简单:
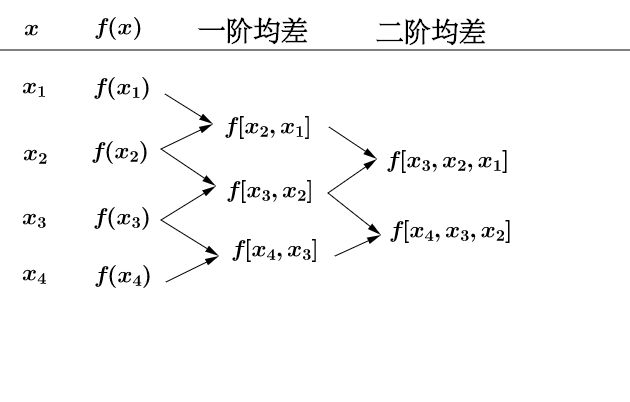
新增一个点,只需要计算相关的差分就可以了:

现有三个点:
| x | f(x) | 一阶差商 | 二阶差商 |
|---|---|---|---|
| 1 | -2 | ||
| 2 | -1 | 1 | |
| 3 | 2 | 3 | 1 |
这最终的插值多项式为:
\[\begin{equation} \begin{aligned} f(x)&=-2 + 1\times(x-1)+1\times(x-1)(x-2)\\ &=x^2-2x-1 \end{aligned} \end{equation}\]增加一个数据点:
| x | f(x) | 一阶差商 | 二阶差商 | 三阶差商 |
|---|---|---|---|---|
| 1 | -2 | |||
| 2 | -1 | 1 | ||
| 3 | 2 | 3 | 1 | |
| 4 | 1 | -1 | -2 | -1 |
当增加以一个点时,插值多项式为:
\[\begin{equation} \begin{aligned} f(x)=&(-2) + 1\times(x-1)+1\times(x-1)(x-2)\\ &+(-1)(x-1)(x-2)(x-3) \end{aligned} \end{equation}\]coding
import matplotlib.pyplot as plt
import numpy as np
import pylab as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
x = [0.4, 0.55, 0.65, 0.80, 0.90, 1.05]
y = [0.41075, 0.57815, 0.69675, 0.88811, 1.02652, 1.25382]
'''计算五次差商的值'''
def five_order_difference_quotient(x, y):
# i 记录计算差商的次数,这里计算五次差商
i = 0
quotient = np.zeros(6)
while i < 5:
j = 5
while j > i:
if i == 0:
quotient[j] = (y[j] - y[j - 1]) / (x[j] - x[j - 1])
else:
quotient[j] = (quotient[j] - quotient[j - 1]) / (x[j] - x[j - 1 - i])
j -= 1
i += 1
# 返回差商值
return quotient
def function(data):
return x[0] + parameters[1] * (data - 0.4) + parameters[2] * (data - 0.4) * (data - 0.55) + \
parameters[3] * (data - 0.4) * (data - 0.55) * (data - 0.65) \
+ parameters[4] * (data - 0.4) * (data - 0.55) * (data - 0.80)
"""计算插值多项式的值和相应的误差"""
def calculate_data(x, parameters):
return_data = []
for data in x:
return_data.append(function(data))
return return_data
def draw(newData):
plt.scatter(x, y, label="离散数据", color="red")
plt.plot(x, newData, label="牛顿插值拟合曲线", color="black")
plt.scatter(0.596, function(0.596), label="预测函数点", color="blue")
plt.title("牛顿插值法")
plt.legend(loc="upper left")
plt.show()
parameters = five_order_difference_quotient(x, y)
yuanzu = calculate_data(x, parameters)
draw(yuanzu)
