描述性统计,即概括性度量。是用来概括、表述事物整体状况以及事物间关联、类属关系的统计方法。通过统计处理可以简洁地用几个统计值来表示一组数据地集中性和离散型 (波动性大小)。
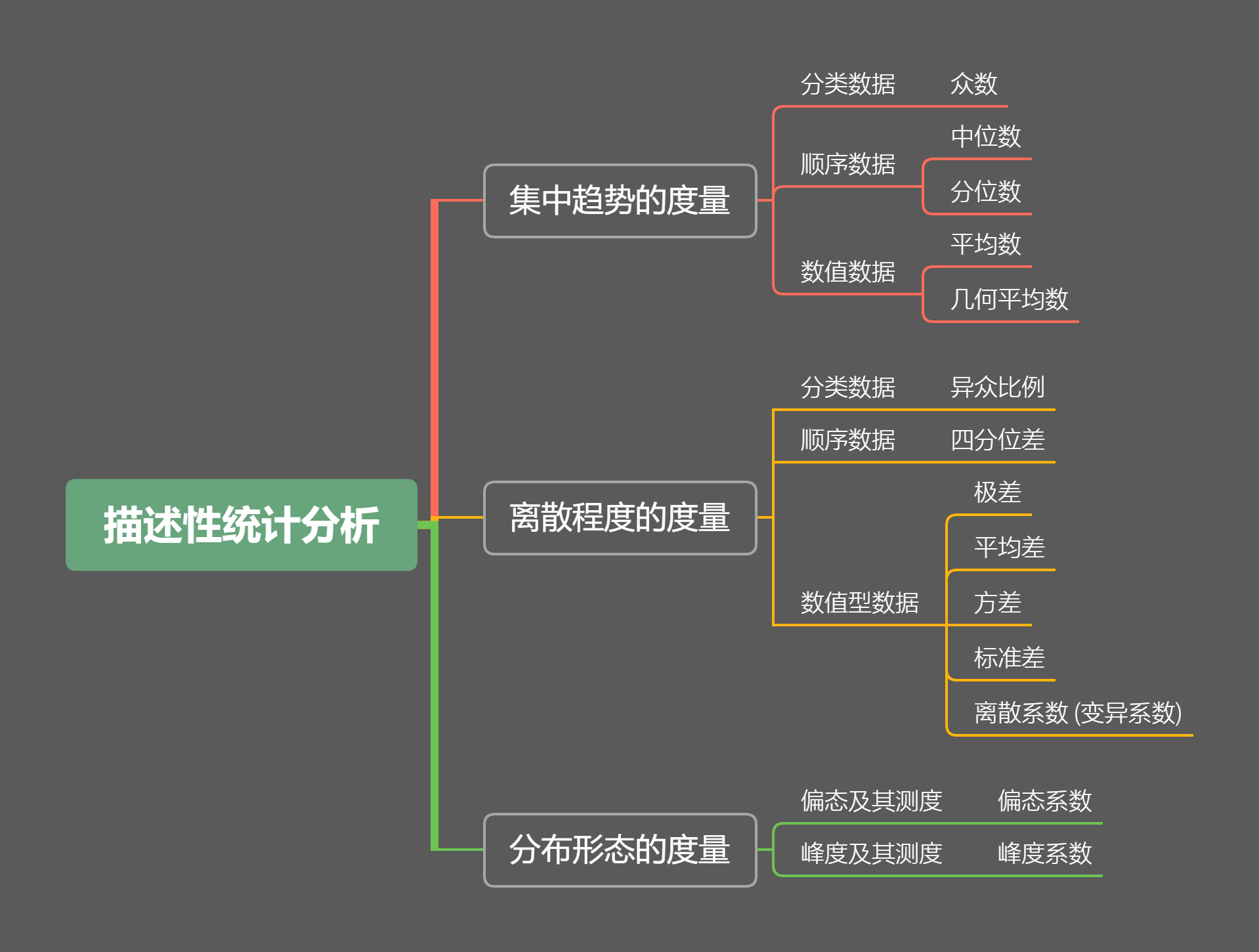
集中趋势
指一组数据向某一中心靠拢的程度,反映了一组数据中心点的位置所在。
众数
- 一组数据中出现次数最多的变量值
- 一般在数据量较大的情况下,众数才有意义
- 众数是一个位置代表值,不受数据中极端值的影响
- 众数可能不存在;也可能存在多个众数
中位数
-
一组数据排序后处于中间位置上的变量值
-
将全部数据等分成两个部分。每部分包含 50% 的数据
-
不适用于分类数据
-
中位数是一个位置代表值,不受数据中极端值的影响
-
中位数位置 = $ \dfrac{n+1}{2} $ , n 为数据个数
-
中位数 \(\begin{equation}M_{e}=\left\{x\left(\frac{n+1}{2}\right), n \text { 为奇数 }, \frac{1}{2}\left\{x\left(\frac{n}{2}\right)+x\left(\frac{n+1}{2}\right), n \text { 为偶数 },\right\}\right.\end{equation}\)
平均数
- 一组数据相加后除以数据的个数得到的结果
- 是集中趋势的最主要测度值
- 主要适用于数值型数据
- 不适用于分类数据和顺序数据
- 是进行统计分析和统计推断的基础
- 从统计学上看,平均数是一组数据的重心所在,是数据误差相互抵消后的必然结果
简单平均数
- 未经分组数据计算的平均数 $\bar{x}$
- $\bar{x}=\frac{x_{1}+x_{2}+\ldots+x_{n}}{n}=\frac{\sum_{i=1}^{n} x_{i}}{n}$
- 加权平均数
- 根据分组数据计算的平均数
- $\bar{x}=\frac{M_{1} f_{1}+M_{2} f_{2}+\ldots+M_{k} f_{k}}{f_{1}+f_{2}+\ldots f_{k}}=\frac{\sum_{i=1}^{k} M_{i} f_{i}}{n}$
几何平均数
- 是 n 个变量值乘积的 n 次方根 G
- 适用于特殊数据的一种平均数,主要用于计算平均比率
- 在实际应用中,主要用于计算现象的平均增长率
- $G=\sqrt[n]{x_{1} \times x_{2} \times \ldots \times x_{n}}=\sqrt[n]{\prod_{i=1}^{n} x_{i}}$
四分位数
-
一组数据排序后处于 25% 和 75% 位置上Q_U的值 $Q_L 和 Q_U$
-
通过 3 个点将全部数据等分成 4 个部分,每个部分包含 25% 的数据
- $Q_{L}$ 位置 $=\frac{n}{4}$
- $Q_{U}$ 位置 $=\frac{3 n}{4}$
众数、中位数和平均数的比较
- 如果数据分布为对称的,则有 $M_{o}=M_{e}=\bar{x}$
- 如果数据分布为左偏的,则有 $\bar{x}<M_{e}<M_{o}$
- 如果数据分布为右偏的,则有 $M_{o}<M_{e}<\bar{x}$
- 当数据呈对称分布或接近对称分布时,应选择
平均数作为集中趋势的代表值 - 当数据呈偏态分布时,尤其是偏斜程度较大时,应考虑
中位数或众数,会有更好的代表性

离散程度
异众比率
-
异众比率又称离异比率或变差比,是指的是非众数的次数与全部变量值总次数的比率,即众数不能代表的那一部分变量值在总体中的比重。
-
异众比率的作用是衡量众数对一组数据的代表程度。异众比率越大,说明非众数组的频数占总频数的比重越大,众数的代表性就越差;异众比率越小,说明非众数组的频数占总频数的比重越小,众数的代表性越好。
-
$V_{r}=\frac{\sum f_{i}-f_{m}}{\sum f_{i}}=1-\frac{f_{m}}{\sum f_{i}}$
$\sum f_{i}$ :为变量值的总频数; $f_m$ : 为众数组的频数。
四分位差
- 也称内距或四分间距,是上四分位数与下四分位数之差 $Q_d$
- 反映了中间 50% 的数据的离散程度,四分位差越小,说明中间的数据越集中;四分位差越大,说明中间的数据越分散
- 不受极值的影响
- 一定程度上说明了中位数对一组数据的代表程度
- $Q_d = Q_u - Q_L$
极差
- 一组数据的最大值与最小值之差,也称全距 R
- 容易受极端值的影响
- $R = max(x_i)-min(x_I)$
平均差
-
也称平均绝对离差,是各变量值与其平均数离差绝对值的平均数 $M_d$
-
反映了每个数据与平均数的平均差异程度,能全面准确地反映一组数据的离散状况,平均差越大,说明数据的离散程度越大;平均差越小,说明数据的离散程度越小
-
未分组情况下 \(\begin{equation}M_{d}=\frac{\sum_{i=1}^{n}\left|x_{i}-\bar{x}\right|}{n}\end{equation}\)
-
分组情况下 \(\begin{equation}M_{d}=\frac{\sum_{i=1}^{k}\left|M_{i}-\bar{x}\right| f_{i}}{n}\end{equation}\)
方差与标准差
方差是各变量值与其平均数离差平方的平均数方差的平方根称为标准差- 能较好地反映出数据的离散程度,是应用最广泛的离散程度的测度值
样本方差是用样本数据个数减1后去除离差平方和- 实际应用中更多使用
标准差 - 未分组数据的
样本方差:$s^{2}=\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}{n-1}$ - 分组数据的
样本方差: $s^{2}=\frac{\sum_{i=1}^{k}\left(M_{i}-\bar{x}\right)^{2} f_{i}}{n-1}$ - 未分组数据的
标准差:$s^{2}=\sqrt{\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}{n-1}}$ - 分组数据的
标准差: $s^{2}=\sqrt{\frac{\sum_{i=1}^{k}\left(M_{i}-\bar{x}\right)^{2} f_{i}}{n-1}}$
离散系数
- 也称为变异系数,是一组数据的标准差与其相应的平均数之比
- 是测度数据离散程度程度的统计量,主要用于比较不同样本数据的离散程度,离散系数大,说明数据的离散程度大;离散系数小,说明数据的离散程度小
- $v_{s}=\frac{s}{\bar{x}}$
相对位置的度量
- 有
平均数和标准差后,可以计算一组数据中各个数据的标准分数,以测度每个数据在该组数据中的相对位置,并用来判断一组数据中是否有离群数据
标准分数
- 是变量值和其平均数的离差除以标准差后的值,也称标准化值 $z$
- $z_{i}=\frac{x_{i}-\bar{x}}{s}$
离散系数
- 也称为变异系数,是一组数据的标准差与其相应的平均数之比
- 是测度数据离散程度程度的统计量,主要用于比较不同样本数据的离散程度,离散系数大,说明数据的离散程度大;离散系数小,说明数据的离散程度小
- $v_{s}=\frac{s}{\bar{x}}$
偏态与峰态(分布形态)
偏态及其测度
- 是对数据分布对称性的测度
- 统计量是
偏态系数$SK$ - 如果一组数据是对称的,则
偏态系数等于 0,不等于 0 则说明分布是不对称的 - 如果
偏态系数大于 1 或者小于 -1,称为高度偏态分布 - 如果
偏态系数在 0.5 ~ 1 或 -1 ~ -0.5 之间,则认为是中等偏态分布 偏态系数越接近 0,偏斜程度越小- 未分组的
偏态系数: $S K=\frac{n \sum\left(x_{i}-\bar{x}\right)^{3}}{(n-1)(n-2) s^{3}}, \quad s^{3}$ 是样本标准差的三次方 - 分组的
偏态系数: $S K=\frac{\sum_{i=1}^{k}\left(M_{i}-\bar{x}\right)^{3} f_{i}}{n s^{3}}, \quad s^{3}$ 是样本标准差的三次方, $M_i$:组中值,$f_i$: 频数
峰态及其测度
- 是对数据分布平峰或尖峰程度的测度
- 统计量是
峰态系数K - 通常是与标准正态分布相比较而言的
- 如果一组数据服从正态分布,则
峰态系数的值等于 0 - 如果
峰态系数的值不等于 0,则可能存在平峰分布或者尖峰分布,需要根据实际标准比较 - 未分组的
峰态系数: $K=\frac{n(n+1) \sum(x-\bar{x})^{4}-3\left[\sum\left(x_{i}-\bar{x}\right)^{2}\right]^{2}(n-1)}{(n-1)(n-2)(n-3) s^{4}}$ - 分组的
峰态系数: $K=\frac{\sum_{i=1}^{k}\left(M_{i}-\bar{x}\right)^{4} f_{i}}{n s^{4}}-3$
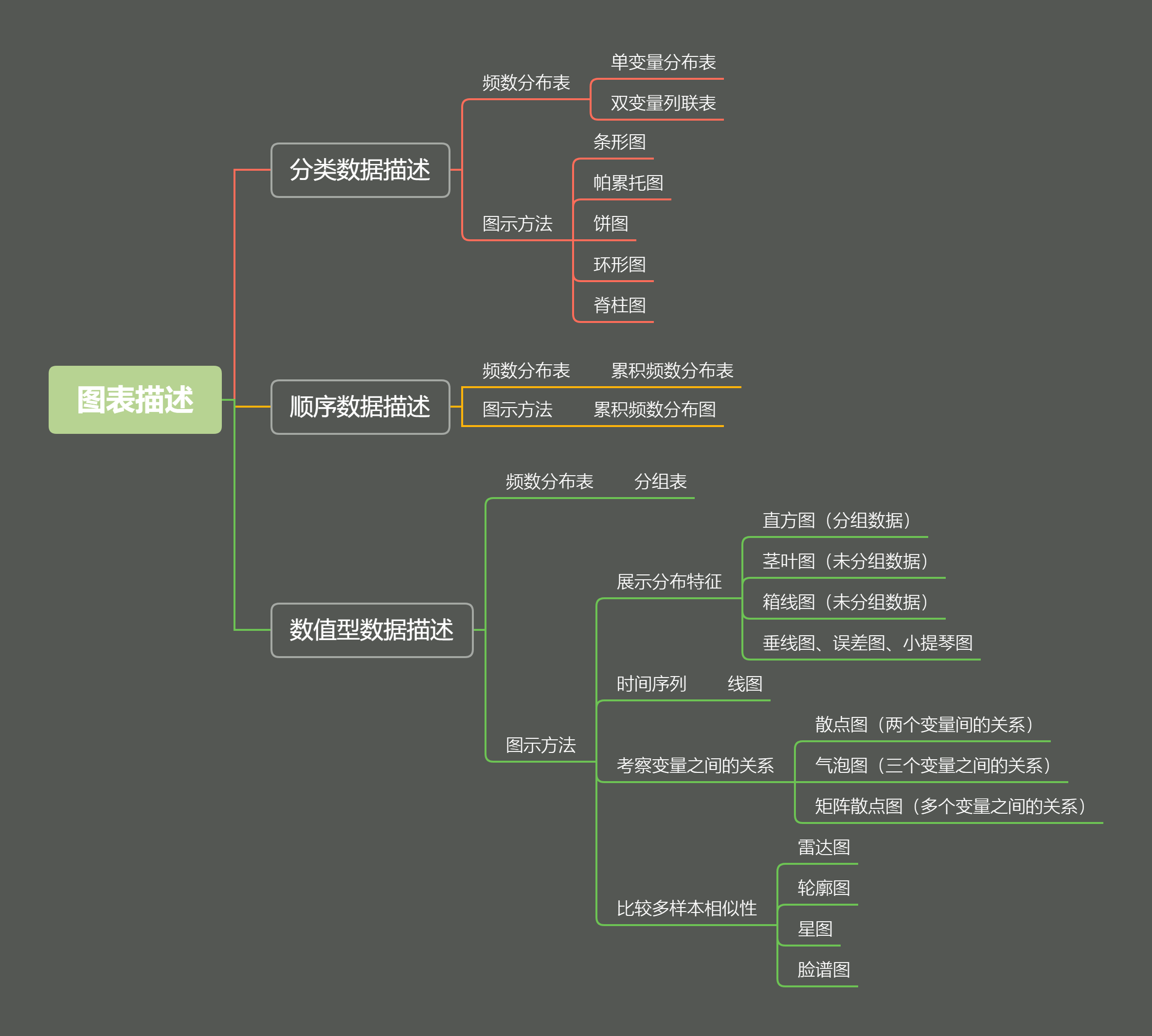
图表描述