错位的梦寐

概率与概率分布

2020-02-13

statistics

概率与概率分布，概率，概率分布，数字特征

一、试验结果及其关系

概率论的研究目的

探寻随机现象在一定概率意义下的变化规律，即统计 规律

概率论的研究方法

随机试验：是导致所有可能观测中有且仅有一个出现 的过程。其特点表现为

  1. 可以在相同的条件下重复地进行（重复性）
  2. 每次试验的可能结果不止一个，并且能事先明确试验的所 有可能结果（明确性）
  3. 进行一次试验之前不能确定哪一个结果会出现（随机性）

概率论通过观察试验结果，探寻随机现象的统计规律

概率论的逻辑思路

  • 首先，描述试验的结果及其关系

  • 其次，度量试验结果的随机不确定性

  • 最后，描述出随机现象变化的统计规律

描述试验结果的若干概念

  • 基本事件（样本点） – 随机试验的每一个“不可能再分”的可能结果
  • 样本空间 – 随机试验的所有基本事件构成的集合，用 \(\Omega\) 表示
  • 随机事件 – 常简称事件，指每次试验可能出现也可能不出现的试 验结果，样本空间中的某些样本点组成的集合，是样 本空间的一个子集，用大写英文字母A、B、C等表示
  • 必然事件 – 每次试验一定出现的试验结果，样本空间的最大子集， 用 \(\Omega\) 表示
  • 不可能事件 – 每次试验一定不出现的事件，样本空间的最小子集， 用 \(\Phi\) 表示
  • 随机变量 – 取值不确定的变量，试验的每一个“不可能再分”的 可能结果，即样本点的数值性描述，用英文大写字母 X、Y、Z等表示

二、试验结果随机不确定性的度量

  • 基本度量方法——概率

  • 什么是概率？

    • 概率与某事件发生的机会、可能性或确定程度有关。
    • 概率(probability) 就是一个数字。介于0和1之间，描 述一个事件发生的可能性大小。
    • 事件A的概率表示为P(A) – 小概率(接近零)的事件很少发生，而大概率(接近1)的 事件则经常发生。

概率的加法公式

公式一

  1. 两个互斥事件之和的概率，等于两个事件 概率之和。设A和B为两个互斥事件，则

    \[\begin{equation}\boldsymbol{P}(A \cup \boldsymbol{B})=\boldsymbol{P}(A)+\boldsymbol{P}(\boldsymbol{B})\end{equation}\]

  2. 事件 \(A_1, A_2, ...,A_n\) 两两互斥，则有

    \[\begin{equation}\begin{array}{l} \boldsymbol{P}\left(\boldsymbol{A}_{1} \cup \boldsymbol{A}_{2} \cup \ldots \cup \boldsymbol{A}_{\mathrm{n}}\right) \\ =\boldsymbol{P}\left(A_{1}\right)+\boldsymbol{P}\left(A_{2}\right)+\ldots+\boldsymbol{P}\left(A_{\mathrm{n}}\right) \end{array}\end{equation}\]

公式二

对任意两个随机事件A和B，它们和的概率 为两个事件各自概率的和减去两个事件交 的概率，即

\[\begin{equation}P(A \cup B)=P(A)+P(B)-P(A \cap B)\end{equation}\]

条件概率

conditional probability

在事件B已经发生的条件下，求事件 A发生的概率，称这种概率为事件B发 生条件下事件A发生的条件概率，记为

\[\begin{equation}P(A | B)=\frac{P(A B)}{P(B)}\end{equation}\]

[例] 100件产品中，有80件正品，20件次品；而 80件正品中有50件一等品，30件二等品。现从这 100件产品中任取1件，问：它是正品的概率？它是 一等品的概率？已知它是正品，是一等品的概率？

解：设事件A表示“取到一等品”，事件B表示“取 到正品”。

\[\begin{equation}\begin{array}{c} P(B)=80 / 100=0.8 \\ P(A B)=50 / 100=0.5 \\ P(A | B)=\frac{50}{80}=\frac{50 / 100}{80 / 100}=\frac{P(A B)}{P(B)} \end{array}\end{equation}\]

概率的乘法公式

  1. 用来计算两事件交的概率 2. 以条件概率的定义为基础
  2. 以条件概率的定义为基础
  3. 设 A 、 B 为两个事件，若 P(B)>0 ， 则 \(P(AB)=P(B)P(A|B)，或P(AB)=P(A)P(B|A)\)

事件的独立性

independence

  • 一个事件的发生与否并不影响另一个事件 发生的概率，则称两个事件独立

  • 若事件 A 与 B 独立，则 \(P(B\|A)=P(B) ， P(A\|B)=P(A)\)

  • 此时概率的乘法公式可简化为 \(P(AB)=P(A)·P(B)\)

  • 推广到多个独立事件，对于任何的\(n<N\)

    \[P(A1 A2 …An)=P(A1)P(A2) … P(An)\]

全概率公式

设事件\(A1，A2，…，An\) 两两互斥， \(A1+A2+…+ An=\Omega\)（满足这两个条件的事件组称为一个完备事 件组），且 \(P(Ai)>0(i=1,2, …,n)\)，则对任意事件B， 有

\[\begin{equation}P(B)=\sum_{i=1}^{n} p\left(A_{i}\right) P\left(B | A_{i}\right)\end{equation}\]

我们把事件\(A_1，A_2，…，A_n\)看作是引起事件B发 生的所有可能原因，事件B 能且只能在原有 \(A_1， A_2，…，A_n\) 之一发生的条件下发生的结果，求 事件B 的概率就是上面的全概率公式

贝叶斯公式(逆概公式)

  1. 与全概公式解决的问题相反，贝叶斯公式是建立 在条件概率基础上的寻找事件发生的原因

  2. 设 n 个事件 \(A1 ， A2 ， … ， An\) 两两互斥，\(A1+A2+…+ An=\Omega\)(满足这两个条件的事件组称为 一个完备事件组)，且\(P(Ai)>0(i=1,2, …,n)\)，则

    \[\begin{equation}P\left(A_{i} | B\right)=\frac{P\left(A_{i}\right) P\left(B | A_{i}\right)}{\sum_{j=1}^{n} p\left(A_{j}\right) P\left(B | A_{j}\right)}\end{equation}\]

贝叶斯公式 (例题分析)

【例】某车间用甲、乙、丙三台机床进行生产，各种机床的次 品率分别为5%、4%、2%，它们各自的产品分别占总产量的 25%、35%、40%，将它们的产品组合在一起，如果取到的一 件产品是次品，分别求这一产品是甲、乙、丙生产的概率

解：设 A1表示“产品来自甲台机床”， A2表示“产品来自 乙台机床”， A3表示“产品来自丙台机床”， B表示“取到次 品”。根据贝叶斯公式有：

\[\begin{equation}\begin{array}{l} P\left(A_{1} | B\right)=\frac{0.25 \times 0.05}{0.0345}=0.3623 \\ P\left(A_{2} | B\right)=\frac{0.35 \times 0.04}{0.0345}=0.406 \\ P\left(A_{3} | B\right)=\frac{0.4 \times 0.02}{0.0345}=0.232 \end{array}\end{equation}\]

随机变量

  1. 一次试验的基本结果（样本点）的数值 性描述，是试验结果的函数。
  2. 一般用 X、Y、Z 来表示
  3. 例如: 投掷两枚硬币出现正面的数量 4. 根据取值情况的不同分为离散型随机变 量和连续型随机变量

随机变量的概率分布

  • 含义
    • 随机变量在其取值范围内，取值与取值概率之间一 一对应的关系，称之为随机变量的概率分布，简称 分布。
    • 注意：概率分布是就样本空间中所有样本点而言的
  • 意义
    • 描述随机变量变化的统计规律。
    • 方便地计算任一事件发生的概率。

离散型随机变量

  1. 随机变量 X 取有限个值或所有取值都可以 逐个列举出来 $X1 , X2，…$
  2. 以确定的概率取这些不同的值

离散型随机变量的概率分布

  1. 列出离散型随机变量X的所有可能取值

  2. 列出随机变量取这些值的概率

  3. 通常用下面的表格来表示

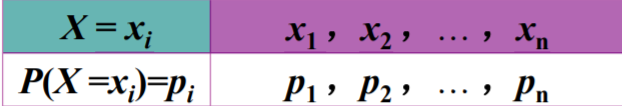
  4. \(P(X =x_i)=p_i\) 称为离散型随机变量的概率函数

    \[\begin{equation}p_{i} \geq 0 \quad \sum_{i=1}^{n} p_{i}=1\end{equation}\]
  • (0—1分布)

  1. 一个离散型随机变量X只取两个可能的值 例如，男性用 1表示，女性用0表示； 合格品用 1 表示，不合格品用0表示

  2. 列出随机变量取这两个值的概率

    \[\begin{equation}P(X=k)=p^{k}(1-p)^{1-k}, k=0,1\end{equation}\]
  • 均匀分布
  1. 一个离散型随机变量取各个值的概率相同
  2. 列出随机变量取值及其取值的概率
  3. 例如，投掷一枚骰子，出现的点数及其出 现各点的概率

离散型随机变量的数学期望

数学期望(expected value)

  1. 在离散型随机变量 $X$ 的一切可能取值的完备 组中，各可能取值 $x_i$与其取相对应的概率 $p_i$乘 积之和
  2. 描述离散型随机变量取值的集中程度
  3. 计算公式为
\[\begin{equation}\begin{aligned}&E(X)=\sum_{i=1}^{n} x_{i} p_{i} \quad(X \text { 取有限个值 })\\&E(X)=\sum_{i=1}^{\infty} x_{i} p_{i} \quad(X \text { 取无穷个值 })\end{aligned}\end{equation}\]

离散型随机变量的方差

方差(variance)

  1. 随机变量 $X$ 的每一个取值与其期望值离差平方 和的数学期望，记为 $D(X) $
  2. 描述离散型随机变量取值的分散程度
  3. 计算公式为、
\[D(X)=E[X-E(X)]^{2} \\若 是离散型随机变量，则\\D(X)=\sum_{i=1}^{\infty}\left[x_{i}-E(X)\right]^{2} \cdot p_{i}\]

几种常见的离散型随机变量的 概率分布

二项分布

二项分布(Binomial distribution)

二项试验(贝努里试验)

  • 二项分布与贝努里试验有关

  • 贝努里试验具有如下属性

    • 试验包含了 n 个相同的试验

    • 每次试验只有两个可能的结果，即“成功”和 “失败”

    • 出现“成功”的概率 p 对每次试验结果是相同 的；“失败”的概率 q 也相同，且 p + q = 1

    • 试验是相互独立的

    • 试验“成功”或“失败”可以计数

二项分布(Binomial distribution)

  1. 进行 n 次重复试验，出现“成功”的次数 的概率分布称为二项分布

二项分布的概率函数

设 X 为 n 次重复试验中事件 A 出现的次数， X 取 $x$ 的概率为

\[\begin{equation}\begin{array}{l} P\{X=x\}=C_{n}^{x} p^{x} q^{n-x} \quad(x=0,1,2, \cdots, n) \\ \text { 式中: } C_{n}^{x}=\frac{n !}{x !(n-x) !} \end{array}\end{equation}\]

二项分布简记为：\(X \sim B(n, p)\)

二项分布的数学期望和方差

  • 二项分布的数学期望为: \(E(X) = np\)

  • 方差为 : \(D(X) = npq\)

泊松分布

泊松分布(Poisson distribution)

  1. 用于描述在一指定时间范围内或在一定的 长度、面积、体积之内每一事件出现次数 的分布
  2. 泊松分布的例子
    • 一个城市在一个月内发生的交通事故次数
    • 消费者协会一个星期内收到的消费者投诉次 数
    • 人寿保险公司每天收到的死亡声明的人数

泊松分布的概率函数

\[\begin{equation}P\{X=x\}=\frac{\lambda \mathrm{e}^{-\lambda}}{x !} \quad(x=0,1,2, \cdots, n)\end{equation}\]

$\lambda$ — 给定的时间间隔、长度、面积、体 积内“成功”的平均数

e = 2.71828

x —给定的时间间隔、长度、面积、体 积内“成功”的次数

泊松分布简记为：\(X \sim P(\lambda)\)

泊松分布的期望和方差

  • 数学期望为 : \(E ( X ) = \lambda\)

  • 方差为 : \(D( X ) = \lambda\)

泊松分布 (作为二项分布的近似)

  • 当试验的次数 n 很大，成功的概率 p 很小时， 可用泊松分布来近似地计算二项分布的概率， 即
\[\begin{equation}C_{n}^{x} p^{x} q^{n-x} \approx \frac{\lambda \mathrm{e}^{-\lambda}}{x !}\end{equation}\]
  • 实际应用中，当 \(P \leq 0.25, \quad n>20, \quad n p \leq 5\) 时， 近似效果良好

超几何分布

超几何分布（hyper geometric distribution）

  • 设有一批产品500个，其中次品有5个。假 定该产品的质量检查采取随机抽取20个产 品进行检查。如果抽到的20个产品中含有 2个或更多不合格产品，则整个500个产品 将会被退回。
  • 这时，人们想知道，该批产品被退回的概 率是多少？
  • 这种概率就满足超几何分布。

连续型随机变量

  1. 连续型随机变量可以取某一区间或整个 实数轴上的任意一个值
  2. 因为它取任何一个特定的值的概率都等 于0，所以不能列出每一个值及其相应的 概率。因此，通常研究它取某一区间值 的概率
  3. 用密度函数和分布函数的形式来描述

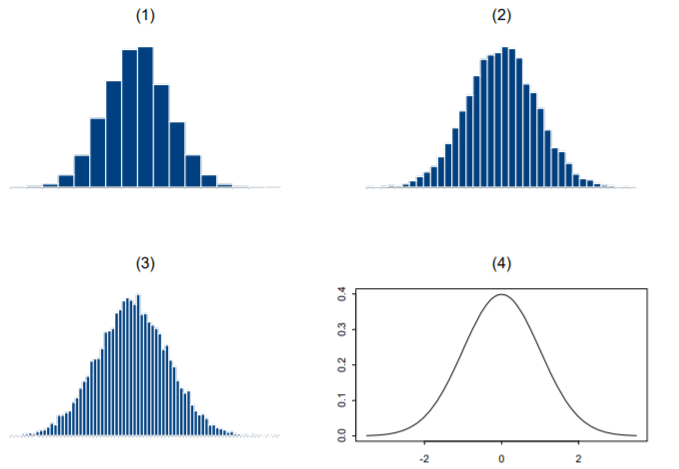
想象连续变量观测值的直方图；如果其纵 坐标为相对频数，那么所有这些矩形条的 高度和为1；完全可以重新设置量纲，使得 这些矩形条的面积和为1。

不断增加观测值及直方图的矩形条的数目， 直方图就会越来越像一条光滑曲线，其下 面的面积和为1。

该曲线即所谓概率密度函数(probability density function，pdf)，简称密度函数或密度。下图为这样形成的密度曲线。

概率密度函数

概率密度函数 (probability density function)

  1. 设 $X$ 为一连续型随机变量，$x$ 为任意实数，$ X$的概率密度函数记为$f(x)$，它满足条件
\[(1) f(x) \geq 0 \\ (2) \int_{-\infty}^{+\infty} f(x) \mathrm{d} x=1$\]

注意：$f(x)$ 本身不是概率，是连续型随机变量 取某一区间值的一种间接表述形式

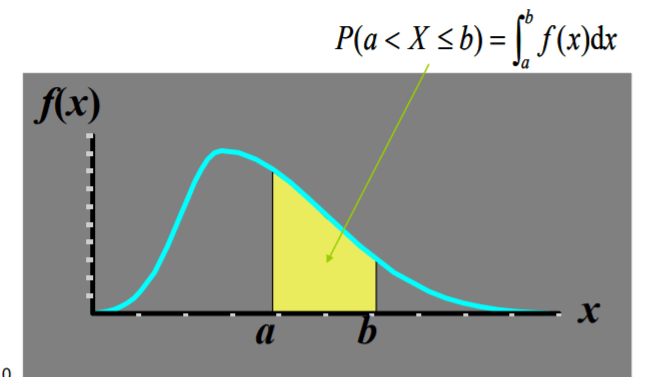
连续型随机变量的概率

在平面直角坐标系中画出 $f(x)$ 的图形，则对 于任何实数\(a<b, \quad P(a<X \leq b)\) 是该曲线下从$a$ 到$ b$的面积

分布函数

分布函数(distribution function)

分布函数的来源 – 如前所述，离散型随机变量的分布用概率函数来描述， 连续型随机变量的分布用密度函数来描述，两者形式 不同，表现各异。为了更方便地表现随机变量的分布， 下面引入分布函数。

分布函数定义为

\[\begin{equation}F(x)=P(X \leq x)=\int_{-\infty}^{x} f(t) \mathrm{d} t \quad(-\infty<x<+\infty)\end{equation}\]

根据分布函数，\(P(a<X<b)\) 可以写为

\[\begin{equation}P(a<X<b)=\int_{a}^{b} f(x) \mathrm{d} x=F(b)-F(a)\end{equation}\]

分布函数与密度函数的图示

  1. 密度函数曲线下的面积等于1
  2. 分布函数是曲线下小于 $x_0$ 的面积

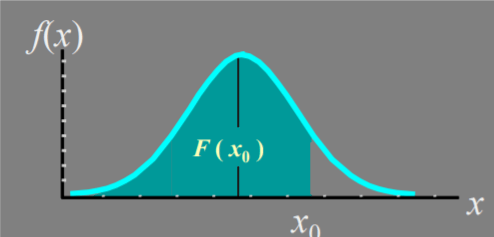
分布函数本身是概率，即事件 $X < x_0$ 发生的 概率

连续型随机变量的期望和方差

  • 连续型随机变量的数学期望为
\[\begin{equation}E(X)=\int_{-\infty}^{+\infty} x f(x) \mathrm{d} x=\mu\end{equation}\]
  • 方差为
\[\begin{equation}D(X)=\int_{-\infty}^{+\infty}[x-E(X)]^{2} f(x) \mathrm{d} x=\sigma^{2}\end{equation}\]

几种常见的连续型随机变量的概率分布

正态分布

正态分布(normal distribution)

描述连续型随机变量分布中最重要的分布

正态分布的重要意义

在随机理论中，正态分布是最重要的一种 分布，理由如下

  • 它是最常见的一种分布，现实中许多随机 变量服从或近似服从正态分布。
  • 在一定的条件下，正态分布是其他分布的 近似分布。
  • 许多有用的分布，特别是小样本的精确分布是由正态分布推导出来的。
  • 是经典统计推断的基础。

正态分布的概率密度函数

\[\begin{equation}\begin{array}{l} f(x)=\frac{1}{\sigma \sqrt{2 \pi}} \mathrm{e}^{\frac{1}{2 \sigma^{2}}(x-\mu)^{2}}, \quad-\infty<x<+\infty \\ f(x)=\text { 随机变量 } X \text { 的频数 } \\ \sigma^{2} \text { = 随机变量 } X \text { 的方差 } \\ \pi=3.14159 ;\;\; \mathrm{e}=2.71828 \\ x=\text { 随机变量 } X \text { 的取值 }(-\infty<x<+\infty) \\ \mu=\text { 随机变量 } X \text { 的均值 } \end{array}\end{equation}\]

正态分布密度函数的性质

  • 概率密度函数在x 轴的上方，即 $f (x)>0$
  • 正态曲线的最高点在均值 $\mu$ 处，它也是分 布的中位数和众数
  • 正态分布是一个分布族，每一特定正态分 布通过均值$\mu$ 和标准差$\sigma$ 来区分。$\mu$ 决定了 图形的中心位置, $\sigma$ 决定曲线的平缓程度， 即宽度
  • 曲线 $f(x)$ 相对于均值$\mu$ 对称，尾端向两个方 向无限延伸，且理论上永远不会与横轴相 交
  • 正态曲线下的总面积等于 1
  • 随机变量的概率由曲线下的面积给出

正态分布的概率

标准正态分布

标准正态分布 (standard normal distribution)

  1. 一般的正态分布取决于均值$\mu$ 和标准差 $\sigma$
  2. 计算概率时 ，每一个正态分布都需要有 自己的正态概率分布表，这种表格是无穷 多的
  3. 若能将一般的正态分布转化为标准正态分 布，计算概率时只需要查一张表

标准正态分布的密度函数

  • 任何一个一般的正态分布，均可通过下面的线 性变换转化为标准正态分布
\[\begin{equation}Z=\frac{X-\mu}{\sigma} \sim N(0,1)\end{equation}\]
  • 标准正态分布的概率密度函数
\[\begin{equation}\varphi(x)=\frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{x^{2}}{2}} \quad, \quad-\infty<x<+\infty\end{equation}\]
  • 标准正态分布的分布函数
\[\begin{equation}\Phi(x)=\int_{-\infty}^{x} \varphi(t) \mathrm{d} t=\int_{-\infty}^{x} \frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{t^{2}}{2}} \mathrm{d} t\end{equation}\]

标准正态分布表的使用

  • 将一个一般的转换为标准正态分布
  • 计算概率时 ，查标准正态概率分布表
  • 对于负的 $x$ ，可由\(\Phi(-x)=1-\Phi(x)\) 得到
  • 对于标准正态分布，即\(X \sim N(0,1)\)，有
\[\begin{equation}\begin{array}{l} P(a \leq \mathrm{X} \leq b)=\Phi(b)-\Phi(a) \\ P(|\mathrm{X}| \leq a)=2 \Phi(a)-1 \end{array}\end{equation}\]
  • 对于一般正态分布，即\(X \sim N(\mu, \sigma)\) 有
\[\begin{equation}P(a \leq X \leq b)=\Phi\left(\frac{b-\mu}{\sigma}\right)-\Phi\left(\frac{a-\mu}{\sigma}\right)\end{equation}\]

几个常用统计量

设 \(X_{1}, X_{2}, \cdots, X_{n}\) 是来自总体的一个样本,\(\boldsymbol{x}_{1}, \boldsymbol{x}_{2}, \cdots, \boldsymbol{x}_{n}\)是这一样本的观察值

样本均值

\[\begin{equation}\bar{X}=\frac{1}{n} \sum_{i=1}^{n} X_{i}\end{equation}\]

其观察值 \(\begin{equation}\bar{x}=\frac{1}{n} \sum_{i=1}^{n} x_{i}\end{equation}\)

样本方差

修正后的样本方差：

\[\begin{equation}S^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}=\frac{1}{n-1}\left(\sum_{i=1}^{n} X_{i}^{2}-n \bar{X}^{2}\right)\end{equation}\]

其观察值

\[\begin{equation}s^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}=\frac{1}{n-1}\left(\sum_{i=1}^{n} x_{i}^{2}-n \bar{x}^{2}\right)\end{equation}\]

样本标准差

\[\begin{equation}S=\sqrt{S^{2}}=\sqrt{\frac{1}{n-1} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}}\end{equation}\]

其观察值

\[\begin{equation}s=\sqrt{\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}\end{equation}\]

协方差

标准差和方差一般是用来描述一维数据的，但现实生活中我们常常会遇到含有多维数据的数据集。比如，一个人的身高和体重是否存在一些联系。协方差就是这样一种用来度量两个随机变量关系的统计量

协方差(covariance)表达了两个随机变量的协同变化关系。

\[\begin{equation}\operatorname{Cov}(X, Y)=E\left[\left(X-\mu_{x}\right)\left(Y-\mu_{y}\right)\right]\end{equation}\]

如果有X,Y两个变量，每个时刻的“X值与其均值之差”乘以“Y值与其均值，

协方差的定义基于期望。根据期望的定义，协方差可以直接用于离散随机变量和连续随机变量。

根据期望的性质，我们可以改写协方差的表达形式:

\[\begin{equation}\begin{aligned} \operatorname{Cov}(X, Y) &=E\left(X Y-X \mu_{X}-Y \mu_{X}+\mu_{X} \mu_{Y}\right) \\ &=E(X Y)-E(X) \mu_{X}-E(Y) \mu_{Y}+\mu_{X} \mu_{Y} \\ &=E(X Y)-E(X) E(Y) \end{aligned}\end{equation}\]

当X和Y独立时，有 \(E(X Y)=E(X) E(Y),\operatorname{Cov}(X, Y)=0\)

相关系数

相关关系是一种非确定性的关系，相关系数是研究变量之间线性相关程度的量。由于研究对象的不同，相关系数有如下几种定义方式。简单相关系数：又叫相关系数或线性相关系数，一般用字母$\rho$ 表示，用来度量两个变量间的线性关系。

\[\begin{equation}\rho=\frac{\operatorname{Cov}(X, Y)}{\sigma_{X} \sigma_{Y}}\end{equation}\]

就是用X、Y的协方差除以X的标准差和Y的标准差

正的协方差表达了正相关性，负的协方差表达了负相关性。对于同样的两个随机变量来说，计算出的协方差越大，相关性越强。

样本 k 阶(原点)矩

\[\begin{equation}A_{k}=\frac{1}{n} \sum_{i=1}^{n} X_{i}^{k}, k=1,2, \cdots\end{equation}\]

其观察值

\[\begin{equation}\alpha_{k}=\frac{1}{n} \sum_{i=1}^{n} x_{i}^{k}, k=1,2, \cdots\end{equation}\]

样本 k 阶中心矩

\[\begin{equation}\boldsymbol{B}_{k}=\frac{1}{\boldsymbol{n}} \sum_{i=1}^{n}\left(\boldsymbol{X}_{i}-\overline{\boldsymbol{X}}\right)^{k}, \boldsymbol{k}=\mathbf{2}, \mathbf{3}, \cdots\end{equation}\]

其观察值: \(\begin{equation}\boldsymbol{b}_{k}=\frac{1}{\boldsymbol{n}} \sum_{i=1}^{n}\left(x_{i}-\overline{\boldsymbol{x}}\right)^{k}, \boldsymbol{k}=2,3, \cdot\end{equation}\)

1阶原点矩 A1 就是样本均值

2阶中心矩 B2 不是样本方差 ,而是 未修正的样本方差

参考

  1. 统计学中「矩」这个概念是怎么引入的？它为什么被称为矩？它与物理意义上的矩有什么相同与不同？
  2. 数据分析必备的统计学知识大梳理！
  3. 概率论11 协方差与相关系数

上一篇 描述性统计分析

下一篇 统计量及其抽样分布

Comments

Content