参数估计

一、参数估计
- 估计量
- 估计值
二、点估计
三、区间估计
四、估计量的评判标准
五、一个总体参数的区间估计
六、两个总体参数的区间估计
九、估计总体均值时样本量的确定
十、估计总体比例时样本量的确定

一、参数估计

如果能够掌握总体的全部数据，那么只需要作一些简单的统计描述，就可以得到所关心的总体特征，比如，总体均值、方差、比例等。但现实情况比较复杂，有些现象的范围比较广，不可能对总体中的每个单位都进行测定。或者有些总体的个体数很多，不可能也没有必要进行一一测定。这就需要从总体中抽取一部分个体进行调查, 进而利用样本提供的信息来推断总体的特征。

参数估计(parameter estimation) 就是用样本统计量去估计总体的参数。比如，用样本均值 $\bar{x}$ 估计总体均值 $\mu$，用样本比例 $p$ 估计总体比例 $π$ ，用样本方差 $s^2$ 估计总体方差 $\sigma^2$ ，等等。如果将总体参数笼统地用一一个符号 $\theta$ 来表示，而用于估计总体参数的统计量用 $\hat{\theta}$ 表示，参数估计也就是如何用 $\theta$ 来估计 $\hat{\theta}$ 。

在参数估计中，用来估计总体参数的统计量称为估计量(estimator)，用符号 $\hat{\theta}$ 表示。样本均值、样本比例、样本方差等都可以是一个估计量。而根据一个具体的样本计算出来的估计量的数值称为估计值(estimated value)。

比如，要估计一个班学生考试的平均分数，从中抽取一个随机样本，全班的平均分数是不知道的，称为参数，用 $\theta$ 表示，根据样本计算的平均分数 $\bar{x}$ 就是一个估计量，用 $\hat{\theta}$ 表示，假定计算出来的样本平均分数为80分，这个80分就是估计量的具体数值，称为估计值。

估计量

在统计学中，估计量是基于观测数据计算一个已知量的估计值的法则

估计量用来估计未知总体的参数，它有时也被称为估计子；一次估计是指把这个函数应用在一组已知的数据集上，求函数的结果。对于给定的参数，可以有许多不同的估计量。我们通过一些选择标准从它们中选出较好的估计量，但是有时候很难说选择这一个估计量比另外一个好。

定义

假设存在一个固定的待估参数 $\theta$。那么”估计量”是样本空间映射到样本估计值的一个函数。$\theta$的一个估计量记为 ${\widehat {\theta }}$ 。

易用随机变量的代数来阐述这个理论：如果用X来标记对应观测数据的随机变量，估计量（本身视为随机变量）的符号表示为该随机变量的函数，$\widehat\theta (X)$ 。对特定观测数据集（即对于$X=x$）而言，其估计值为一固定值${\widehat {\theta }}(x)$ 。通常使用简化标记 ${\widehat {\theta }}$ 表示随机变量，但这容易造成误解。

误差

对于一个给定样本$x$，估计量 $\widehat {\theta }$ 的”误差“定义为 $\begin{equation}e(x)=\hat{\theta}(x)-\theta\end{equation}$ 其中 ${\displaystyle \theta }$ 是待估参数。注意误差 $e$ 不仅取决于估计量（估计公式或过程），还取决于样本。

均方误差

估计量 ${\displaystyle {\hat {\theta }}}$ 的均方误差被定义为误差的平方的期望值，即为： $\begin{equation}M S E(\hat{\theta})=E\left[(\hat{\theta}(x)-\theta)^{2}\right]\end{equation}$ 它用来显示估计值的集合与被估计单个参数的平均差异。

试想下面的类比：假设“参数”是靶子的靶心，“估计量”是向靶子射箭的过程，而每一支箭则是“估计值”（样本）。那么，高均方误差就意味着每一支箭离靶心的平均距离较大，低均方误差则意味着每一支箭离靶心的平均距离较小。箭支可能集聚，也可能不。比如说，即使所有箭支都射中了同一个点，同时却严重偏离了靶子，均方误差相对来说依然很大。然而要注意的是，如果均方误差相对较小，箭支则更有可能集聚（而不是离散）。

行为特性

判断一个估计量“好坏”，至少可以从以下三个方面来考虑：无偏性、有效性、一致性。

估计值

在数理统计中，一般用子样观测值求出的统计量来估计总体的一个未知参数，此统计量称为参数的估计量。子样一组观测值所对应估计量的值，称为参数的估计值。

估计值亦称估计量的实现，简称估计，是指估计量的具体数值。在进行理论分析和一般性讨论时，未知参数θ的估计量 $\theta=T\left(X_{1}, X_{2}, \ldots, X_{n}\right)$ 作为随机样本的函数，是随机变量；在实际应用中，样本是一组统计数据 $x_{1}, x_{2}, \ldots, x_{n}$ (随机样本的实现——样本值)，而估计量 $\theta$ 相应地取一具体值 $\theta=T\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ ，即为 $\theta$ 的估计值。

参数估计的方法有点估计和区间估计两种

二、点估计

点估计（Point estimation）

点估计也称定值估计，它是以抽样得到的样本指标作为总体指标的估计量，并以样本指标的实际值直接作为总体未知参数的估计值的一种推断方法。

点估计的方法

点估计的方法有矩估计法、顺序统计量法、最大似然法、最小二乘法等。

矩估计法。

在统计学中，矩是指以期望为基础而定义的数字特征，一般分为原点矩和中心矩。

设 $X$ 为随机变量，对任意正整数k，称 $E\left(X^{k }\right)$ 为随机变量 $X$ 的 k 阶原点矩，记为： $m_k = E\left(X^{k }\right)$ 当k＝1时， $m_1 = E(X) = \mu$ 可见一阶原点矩为随机变量X的数学期望。

把 $C_{k }=E[X-E(X)]^{k}$ 称为以$E(X)$为中心的k阶中心矩。

显然，当k＝2时 $C_{2 }=E[X-E(X)]^{2}$ 可见二阶中心矩为随机变量X的方差。

　矩估计法简便、直观，比较常用，但是矩估计法也有其局限性。首先，它要求总体的k阶原点矩存在，若不存在则无法估计；其次，矩估计法不能充分地利用估计时已掌握的有关总体分布形式的信息。

通常设 $θ$ 为总体X的待估计参数，一般用样本 $X_{1}, X_{2}, \cdots, X_{n}$ 构成一个统计量 $\hat{\theta}=\hat{\theta}\left(X_{1}, X_{2}, \Lambda, X_{n}\right)$ 来估计 $θ$ 则称 $\hat{\theta}$ 为θ的估计量。对于样本的一组数值 $x_{1}, x_{2}, \cdots, x_{n}$ 称θ的估计值。于是点估计即是寻求一个作为待估计参数θ的估计量 $\hat{\theta}(x_{1}, x_{2}, \cdots, x_{n})$ 的问题。但是必须注意，对于样本的不同数值，估计值是不相同的。

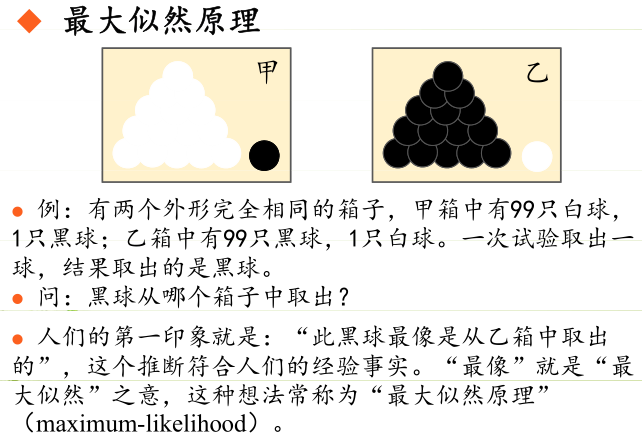
极大似然估计

最大似然估计（英语：maximum likelihood estimation，缩写为MLE），也称极大似然估计

最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

原理：极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

如果总体X为离散型

假设分布率为 $P=p(x ; \theta)$，x 是发生的样本，$θ$ 是代估计的参数，$p(x ; \theta)$表示估计参数为θθ时，发生x的的概率。

那么当我们的样本值为：$x_{1}, x_{2}, \ldots, x_{n}$ 时， $\begin{equation}L(\theta)=L\left(x_{1}, x_{2}, \ldots, x_{n} ; \theta\right)=\prod_{i=1}^{n} p\left(x_{i} ; \theta\right)\end{equation}$ 其中$L(θ)$ 成为样本的似然函数。

假设 $\begin{equation}L\left(x_{1}, x_{2}, \ldots, x_{n} ; \hat{\theta}\right)=\max _{\theta \in \Theta} L\left(x_{1}, x_{2}, \ldots, x_{n} ; \theta\right)\end{equation}$ 有 $\hat{\theta}$ 使得$ L(θ)$ 的取值最大，那么 $\hat{\theta}$ 就叫做参数 $\theta$ 的极大似然估计值。

如果总体X为连续型

基本和上面类似，只是概率密度为 $f(x ; \theta)$ ，替代p。 $\begin{equation}L(\theta)=\prod_{i=1}^{n} f\left(x_{i} ; \theta\right)\end{equation}$ 解法

构造似然函数 $L(θ)$
取对数：$lnL(θ)$
求导，计算极值
解方程，得到 $θ$

三、区间估计

用点估计 $\hat{\theta}\left(X_{1}, X_{2}, \ldots, X_{n}\right)$ 来估计总体的未知参数 $\theta$ 一旦我们获得了样本观察值 $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$

将它代入 $\hat{\theta}\left(X_{1}, X_{2}, \ldots, X_{n}\right)$ 即可得到 $θ$ 的一个估计值。这很直观，也很便于使用。但是，点估计值只提供了$ $ 的一个近似值，并没有反映这种近似的精确度。同时，由于 $θ$ 本身是未知的，我们也无从知道这种估计的误差大小。因此，我们希望估计出一个真实参数所在的范围，并希望知道这个范围以多大的概率包含参数真值，这就是参数的区间估计问题。

定义

设总体 $X \sim F(x ; \theta)$ ，$\theta$ 是待估计参数，若对给定的 $\alpha (0<\alpha <1)$ , 存在两个统计量：$\underline{\theta}=\underline{\theta}\left(X_{1}, X_{2}, \cdots, X_{n}\right), \quad \bar{\theta}=\bar{\theta}\left(X_{1}, X_{2}, \cdots, X_{n}\right)$ 使得 $P\{\underline{\theta}<\theta<\overline{\boldsymbol{\theta}}\}=1-\alpha, \quad \boldsymbol{\theta} \in \Theta$

则称随机区间 $(\underline{\theta}, \bar{\theta})$ 为 $\theta$ 的置信度为 $1-\alpha$ 的置信区间， $\underline{\theta}, \bar{\theta}$ 分别成为置信下限和置信上限， $1-\alpha$ 成为置信度或置信水平。

区间估计的几点说明：

置信区间的长度 $\bar{\theta}-\underline{\theta}$ 反映了估计的精度， $\bar{\theta}-\underline{\theta}$ 越小，估计精度越高。
$\alpha$ 反映了估计的可信度。$\alpha$ 越小，$1-\alpha$ 越大，估计的可信度越高；但通常会导致 $\bar{\theta}-\underline{\theta}$ 增大。从而导致估计的精度降低。
$\alpha$ 给定后，置信区间的选取不唯一，通常选取 $\bar{\theta}-\underline{\theta}$ 最小的区间。

值得注意的是，置信区间 $\left(\hat{\theta}_{1}, \hat{\theta}_{2}\right)$ 是一个随机区间，对于给定的样本 $\left(X_{1}, X_{2}, \ldots, X_{n}\right)$，可能包含未知参数， $\left(\hat{\theta}_{1}, \hat{\theta}_{2}\right)$ 也可能不包含 $\left(\hat{\theta}_{1}, \hat{\theta}_{2}\right)$ 。但在重复取样下，将得到许多不同的区间$\hat{\theta}_{1}\left(x_{1}, x_{2}, \ldots, x_{n}\right), \hat{\theta}_{2}\left(x_{1}, x_{2}, \ldots, x_{n}\right)$，根据贝努利大数定律，这些区间中大约有$100(1−\alpha)$ 的区间包含未知参数 $\theta$ 。

置信区间的含义

以$\alpha=0.01$为例，此时置信度为99。假设反复抽取样本1000次，则得到1000个随机区间 $\left(\hat{\theta}_{1}, \hat{\theta}_{2}\right)$ ,在这1000个区间中，包含值的大约有990个，而不包含 $\theta$ 值的大约有10个。

枢轴量

定义：设总体 $X$ 有概率密度（或分布律）$f(x;θ)$ ，其中 $θ$ 是待估的未知参数。设 $X_1,…,X_n$ 是一个样本，记： $\begin{equation}U=U\left(X_{1}, \ldots, X_{n} ; \theta\right)\end{equation}$ 为样本和待估参数 $θ$ 的函数，如果 $U$ 的分布已知，不依赖与任何参数，就称 $U$ 为枢轴量。

由上述定义可以看出枢轴量的几个特点：

与某个待估参数有关（事实上枢轴量法主要被用于未知参数的区间估计）；
本身含有未知参数（待估参数），因此不具有“可观察性”，也就是说即使选定了样本也无法计算出确定的值；
其分布是明确的（有具体的数学公式，不包含未知参数）。

一个比较常见的例子：均值或方差未知的正态分布转换成标准正态分布时，随机变量中还是包含未知参数，但是其分布中却不包含任何未知参数。因此标准化之后的随机变量是一个枢轴量。

一般正态分布与标准正态分布之间的关系：当$X \sim N(\mu, \sigma) \text { 时, } \frac{X-\mu}{\sigma} \sim N(0,1)$

枢轴量法需要解决的问题

枢轴量法作为区间估计的主要方法，要求解的问题如下：

设总体 $X$ 的分布含有未知参数 $θ，X_1,…,X_n$ 是一次抽样得到的样本。

如何给出 $θ$ 的置信水平为$1−α$ 的双侧置信区间(或单侧置信上限、单侧置信下限)？

区间估计的步骤

1.构造一个与 $\theta$ 有关的函数 $U$ (又称为枢轴变量)

(1) $U$ 不含其他参数，(2)已知 $U$ 的分布

2.对给定的 $\alpha (0<\alpha<1)$，求 $a,b$ 使得 $\begin{equation}P\{a \leq U \leq b\}=1-\alpha\end{equation}$

3 解不等式 $a \leq U \leq b \Leftrightarrow T_{1} \leq \theta \leq T_{2}$ ,得到区间$[\hat{\theta}_{1}, \hat{\theta}_{2}]$

例设 $X_{1}, X_{2}, \cdots, X_{n}$ 来自总体 $X \sim N(\mu, 1)$ 的样本，求$\mu$ 的置信度为 $1-\alpha$ 的置信区间

解：

$\mu$ 的无偏估计为 $\bar{X}$ ,且 $\begin{equation}\bar{X} \sim N\left(\mu, \frac{1}{n}\right) \hookrightarrow \frac{\bar{X}-\mu}{1 / \sqrt{n}} \sim N(0,1)\end{equation}$

即 $U =\frac{\bar{X}-\mu}{1 / \sqrt{n}}$

由此得到 $P\left\{-u_{1-a/2}<\frac{\bar{X}-\mu}{1 / \sqrt{n}}<u_{1-\alpha/2} \right\}=1-\alpha$

即 $P\left\{\bar{X}-\frac{1}{\sqrt{n}} u_{1-\alpha/2}<\mu<\bar{X}+\frac{1}{\sqrt{n}} u_{1-\alpha/2},\right\}=1-\alpha$

所以 $\mu$ 的置信度为 $1-\alpha$ 的置信区间为： $\begin{equation}\left(\bar{X}-\frac{1}{\sqrt{n}} u_{1-\alpha / 2}, \bar{X}+\frac{1}{\sqrt{n}} u_{1-\alpha / 2}\right)\end{equation}$

枢轴量的构造

枢轴量 $U(X_1,…,X_n;θ)$ 的构造，通常从$θ$ 的点估计 $\hat{\theta}$ (如极大似然估计，矩估计等)出发，根据 $θ$ 的分布(或包含 $θ$ 的函数的分布)进行改造而得。

常见枢轴量

从区间估计的求解流程和上面的例子可以看出来，如果要使用枢轴量法来作区间估计，找到合适的枢轴量是关键。

下面所有的枢轴量都是跟总体均值和方差有关的，因此我们能估计的也仅限于这两个参数；

总体方差已知和未知是两种不同的情况，构造出来的枢轴量属于不同的分布；

具有两个正态总体时，可以估计两个不同总体均值的差或方差的比值.

1、单个正态总体 $N(μ,σ^2)$)情形

(1) $μ$ 的枢轴量：

$σ^2$已知时 : $\frac{\bar{X}-\mu}{\sigma / \sqrt{n}} \sim N(0,1)$
$σ^2$未已知时：$\frac{\bar{X}-\mu}{S / \sqrt{n}} \sim t(m-1)$ 用样本方差代替总体标准差

(2) $σ^2$ 的枢轴量：

$μ$ 未知: $\frac{(n-1) S^{2}}{\sigma^{2}} \sim \chi^{2}(n-1)$

2、二个正态总体 $N\left(\mu_{1}, \sigma_{1}^{2}\right), N\left(\mu_{2}, \sigma_{2}^{2}\right)$ 的情形

(1) $μ_1−μ_2$的枢轴量：

$σ_1^2,σ_2^2$已知时 $\begin{equation}\frac{(\bar{X}-\bar{Y})-\left(\mu_{1}-\mu_{2}\right)}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}} \sim N(0,1)\end{equation}$
$σ_1^2,σ_2^2$ 未知时 $\begin{equation}\frac{(\bar{X}-\bar{Y})-\left(\mu_{1}-\mu_{2}\right)}{S_{w} \sqrt{1 / n_{1}+1 / n_{2}}} \sim t\left(n_{1}+n_{2}-2\right)\end{equation}$

其中 : $S_{w}^{2}=\frac{\left(n_{1}-1\right) S_{1}^{2}+\left(n_{2}-1\right) S_{2}^{2}}{n_{1}+n_{2}-2}, S_{w}=\sqrt{S_{w}^{2}}$

(2) $\frac{\sigma_{1}^{2}}{\sigma_{2}^{2}}$ 的枢轴量

$μ_1,μ_2$未知 $\begin{equation}\frac{S_{1}^{2} / S_{2}^{2}}{\sigma_{1}^{2} / \sigma_{2}^{2}} \sim F\left(n_{1}-1, n_{2}-1\right)\end{equation}$ 3、其他总体均值的区间估计

设总体 $X$ 的均值为 $μ$ ，方差为 $σ^2$，非正态分布或不知分布形式. 样本为 $X_1,…,X_n$.

当n充分大(一般n>30)时，有中心极限定理知，$\bar{X} \sim N\left(\mu, \sigma^{2} / n\right)$ ，因此 $\begin{equation}\frac{\bar{X}-\mu}{\sigma / \sqrt{n}} \sim N(0,1)\end{equation}$ 以上分布为近似分布

当 $σ^2$ 已知时，μμ的置信水平为 $1−α$ 的近似置信区间为 $\begin{equation}\left(\bar{X}-z_{\alpha / 2} \sigma / \sqrt{n}, \bar{X}+z_{\alpha / 2} \sigma / \sqrt{n}\right)\end{equation}$
当 $σ^2$ 未知时，以样本方差 $S^2$代入，得近似置信区间为 $\begin{equation}\left(\bar{X}-z_{\alpha / 2} S / \sqrt{n}, \bar{X}+z_{\alpha / 2} S / \sqrt{n}\right)\end{equation}$

正态总体参数的区间估计

一个总体 $N\left(\mu, \sigma^{2}\right)$ 的情形

1、方差 $\sigma^{2}$ 未知，$\mu$ 的置信区间

设 $X_{1}, X_{2}, \cdots, X_{n}$ 是总体 $X \sim N\left(\mu, \sigma^{2}\right)$ 的样本， $\sigma^{2}$ 未知，求 $\mu$ 的置信度为 $1-\alpha$ 的置信区间

因为 $\mu$ 的 MLE 是 $\bar{X}$ 选取枢轴变量 $\begin{equation}\frac{\bar{X}-\mu}{\sigma / \sqrt{n}}\end{equation}$ 因为枢轴变量的要求是：样本和待估参数的函数，而且它的分布要已知，且不能含有任何未知参数，上面的式子中 $\sigma$ 是未知的，和枢轴变量的要求不吻合，解决方法，用样本的标准差代替未知的整体的标准差，即 $\begin{equation}\frac{\bar{X}-\mu}{S / \sqrt{n}}\end{equation}$ $S$ 样本标准差

找出上面的函数的已知分布，满足自由度为 $n-1$ 的 $t$ 分布，即 $\begin{equation}\frac{\bar{X}-\mu}{S / \sqrt{n}}\sim t(n-1)\end{equation}$ 既有： $\begin{equation}P\left(-t_{1-\frac{\alpha}{2}}(n-1)<\frac{\bar{X}-\mu}{S / \sqrt{n}}<t_{1-\frac{\alpha}{2}}(n-1)\right\}=1-\alpha\end{equation}$ 解： $\begin{equation}-t_{1-\frac{\alpha}{2}}(n-1)<\frac{\boldsymbol{X}-\mu}{\boldsymbol{S} / \sqrt{\boldsymbol{n}}}<t_{1- \frac{\alpha}{2}}(n-1)\end{equation}$ 得 $\mu$ 的置信度为 $1-\alpha$ 的置信区间为 $\begin{equation}\left(\bar{X}-t_{1- \frac{\alpha}{2}}(n-1) \frac{S}{\sqrt{n}},\bar{X}+t_{1- \frac{\alpha}{2}}(n-1) \frac{S}{\sqrt{n}}\right)\end{equation}$ 2、$\mu$ 未知，方差 $\sigma^{2}$ 的置信区间

设 $X_{1}, X_{2}, \cdots, X_{n}$ 是总体 $X \sim N\left(\mu, \sigma^{2}\right)$ 的样本， $\mu$ 未知，求 $\sigma^{2}$ 的置信度为 $1-\alpha$ 的置信区间

$\sigma^{2}$ 的MLE 是 $S^2$ (修正后的样本方差)，选取枢轴变量 $\begin{equation}\frac{n \tilde{S}^{2}}{\sigma^{2}}=\frac{(n-1) S^{2}}{\sigma^{2}}\end{equation}$ （上面的式子由样本方差和修正后的样本方差关系转换得到的）

此时的分布：服从自由度为$n-1$ 的卡方分布，即 $\begin{equation}\frac{(n-1) S^{2}}{\sigma^{2}}-\chi^{2}(n-1)\end{equation}$

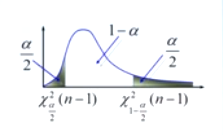
既有 $\begin{equation}P\left\{\chi_{\frac{\sigma}{2}}^{2}(n-1)<\frac{(n-1) S^{2}}{\sigma^{2}}<\chi_{1- \frac{\alpha}{2}}^{2}(n-1)\right\}=1-\alpha\end{equation}$

$\begin{equation}\chi_{\frac{\alpha}{2}}^{2}(n-1)<\frac{(n-1) S^{2}}{\sigma^{2}}<\chi_{1-\frac{\alpha}{2}}^{2}(n-1)\end{equation}$ 得到 $\sigma^2$ 的置信度为 $1-\alpha$ 的置信区间为 $\begin{equation}\left(\frac{(n-1) S^{2}}{X_{1- \frac{\alpha}{2}}^{2}(n-1)}, \frac{(n-1) S^{2}}{X_{\frac{\alpha}{2}}^{2}(n-1)}\right)\end{equation}$

四、估计量的评判标准

1 无偏性 2 有效性 3 一致性

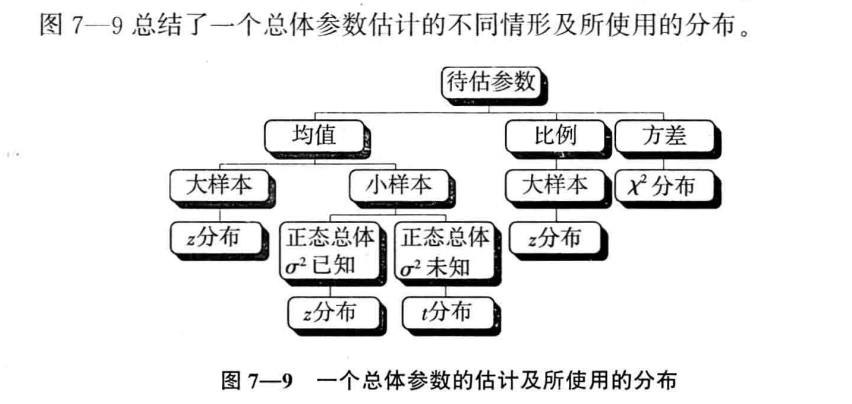
五、一个总体参数的区间估计

1、总体均值的区间估计

正态总体、方差已知，或非正态总体、大样本

例题：

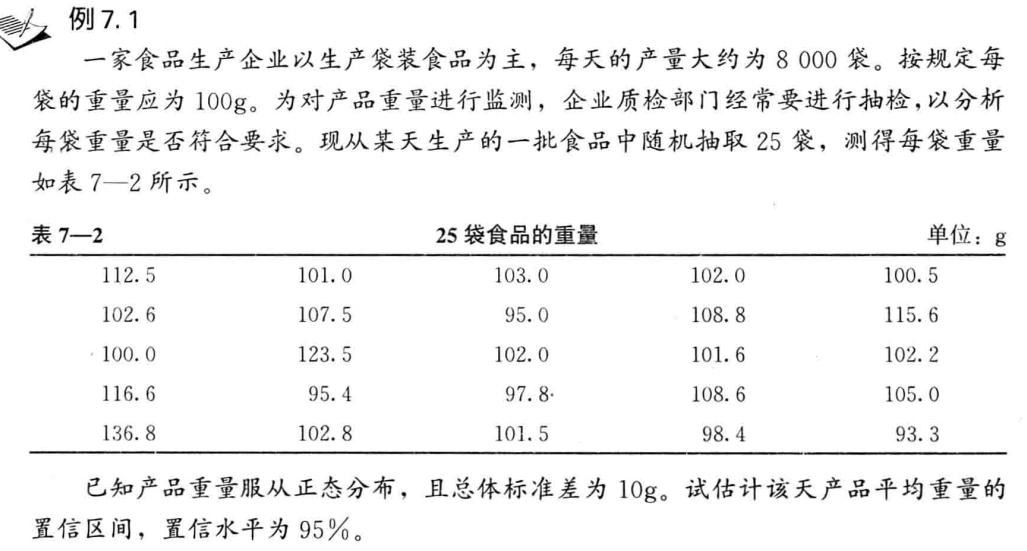
正态总体、方差未知、小样本

例题：

总结

2、总体比例的区间估计

例题：

3、总体方差分布的区间估计

例题:

总结

六、两个总体参数的区间估计

对于两个总体，所关心的参数主要有两个总体的均值之差 $\mu_1-\mu_2$ , 两个总体的比例之差 $\pi_1 -\pi_2$ 、两个总体的方差之比 $\sigma_1^2 / \sigma_2^2$ 等。

1、两个总体均值之差区间估计

设两个总体的均值分别为 $\mu_1$ 和 $\mu_2$ .从两个总体中分别抽取样本量为$n_1$ 和 $n_1$ 的两个随机样本，其样本均值分别为 $\bar{x_1}$ 和 $\bar{x_2}$ 。两个总体均值之差 $μ_1 - μ_2$ 的估计量显然是两个样本的均值之差 $\bar{x_1}-\bar{x_2}$ 。

两个总体均值之差的估计：独立样本

(1) 大样本的估计

(2) 小样本的估计

在两个样本都为小样本的情况下，为估计两个总体的均值之差，需要作出以下

假定:

两个总体都服从正态分布。
两个随机样本独立地分别抽自两个总体。

在上述假定下，无论样本量的大小，两个样本均值之差都服从正态分布。当两个总体方差 $\sigma_1^2$ 和 $\sigma_1^2$ 已知时，可用式(7.13) 建立两个总体均值之差的置信区间。当 $\sigma_1^2$ 和 $\sigma_1^2$ 未知时，有以下几种情况。

当两个总体的方差 $\sigma_1^2$ 和 $\sigma_1^2$ 未知但相等时

例题：

当两个总体的方差 $\sigma_1^2$ 和 $\sigma_1^2$ 未知并且不相等时

例题：

匹配样本

在例7.7中使用的是两个独立的样本，但使用独立样本来估计两个总体均值之差存在着潜在的弊端。比如，在对每种方法随机指派12个工人时，偶尔可能会将技术比较差的12个工人指定给方法1，而将技术较好的12个工人指定给方法2.这种不公平的指派可能会掩盖两种方法组装产品所需时间的真正差异。为解决这一问题，可以使用匹配样本(matchedsample).即一个样本中的数据与另一个样本中的数据相对应。比如，先指定12个工人用第-一种方法组装产品，然后再让这12个工人用第二种方法组装产品，这样得到的两种方法组装产品的数据就是匹配数据。匹配样本可以消除由于样本指定的不公平造成的两种方法组装时间上的

例题：