假设检验

参数估计和假设检验
假设检验( hypothesis testing)
一个总体参数的检验
两个总体参数的检验
检验中的匹配样本

参数估计和假设检验

参数估计( parameter estimation) 和 假设检验 ( hypothesis testing) 是统计推断的两个组成部分，它们都是利用样本对总体进行某种推断，但推断的角度不同。参数估计讨论的是用样本统计量估计总体参数的方法，总体参数 $μ$ 在估计前是未知的。而在假设检验中，则是先对 $μ$ 的值提出一个假设，然后利用样本信息去检验这个假设是否成立。

假设检验( hypothesis testing)

包括参数和非参数检验：

参数假设检验（parametric test）：总体的分布形式已知，需要对总体的未知参数进行假设检验。
非参数假设检验（non-parametric test）：对总体分布形式所知甚少，需对未知分布函数的形式及其他特征进行假设检验。

参数假设检验举例

例1: 根据1989年的统计资料，某地女性新生儿的平均体重为3190 克。为判断该地1990年的女性新生儿体重与1989年相比有无显著差异，从该地1990年的女性新生儿中随机抽取30人，测得其平均体重为3210克。从样本数据看，1990年女新生儿体重比 1989年略高，但这种差异可能是由于抽样的随机性带来的，也许这两年新生儿的体重并没有显著差异。究竟是否存在显著差异？可以先假设这两年新生儿的体重没有显著差异，然后利用样本信息检验这个假设能否成立。这是一个关于总体均值的假设检验问题。

假设检验的原理

小概率原理。假设检验的基本思想是概率性质的反证法。(不同于纯数学中的反证法)

什么是小概率？

概率是0～1之间的一个数，因此小概率就是接近0的一个数
著名的英国统计家 Ronald Fisher 把 20 分之 1 作为标准，也就是0.05，从此0.05或比0.05小的概率都被认为是小概率
Fisher没有任何深奥的理由解释他为什么选择0.05，只是说他忽然想起来的

什么是小概率原理

小概率原理——发生概率很小的随机事件（小概率事件）在一次实验中几乎是不可能发生的。
根据这一原理，可以先假设总体参数的某项取值为真，也就是假设其发生的可能性很大，然后抽取一个样本进行观察，如果样本信息显示出现了与事先假设相反的结果且与原假设差别很大，则说明原来假定的小概率事件在一次实验中发生了，这是一个违背小概率原理的不合理现象，因此有理由怀疑和拒绝原假设；否则不能拒绝原假设。
检验中使用的小概率是检验前人为指定的。

小概率原理举例

某工厂质检部门规定该厂产品次品率不超过4％方能出厂。今从1000件产品中抽出10件，经检验有4件次品，问这批产品是否能出厂?

如果假设这批产品的次品率P≤4％，则可计算事件 “抽10件产品有4件次品”的出现概率为：

\[\begin{equation}P_{10}(4)=C_{10}^{4}(0.04)^{4}(1-0.04)^{6}=0.00042\end{equation}\]

可见，概率是相当小的，1万次实验中可能出现4次，然而概率如此小的事件，在一次实验中居然发生了，这是不合理的，而不合理的根源在于假设次品率 P≤4％，因而认为假设次品率P≤4％是不能成立的，故按质检部门的规定，这批产品不能出厂。

假设检验的基本思想

假设检验的两个特点

第一，假设检验采用逻辑上的反证法，即为了检验一个假设是否成立，首先假设它是真的，然后对样本进行观察，如果发现出现了不合理现象，则可以认为假设是不合理的，拒绝假设。否则可以认为假设是合理的，接受假设。
第二，假设检验采用的反证法带有概率性。所谓假设的不合理不是绝对的，而是基于实践中广泛采用的小概率事件几乎不可能发生的原则。至于事件的概率小到什么程度才算是小概率事件，并没有统一的界定标准，而是必须根据具体问题而定。如果一旦判断失误，错误地拒绝原假设会造成巨大损失，那么拒绝原假设的概率就应定的小一些；如果一旦判断失误，错误地接受原假设会造成巨大损失，那么拒绝原假设的概率就应定的大一些。
小概率通常用 $α$ 表示，又称为检验的显著性水平。通常取 $α$ ＝0.05 或 $α$ ＝0.01，即把概率不超过 0.05 或 0.01 的事件当作小概率事件。

原假设和备择假设

假设检验中，我们称作为检验对象的待检验假设为原假设或零假设，用 $H_0$表示。原假设的对立假设称为备择假设或备选假设，用 $H_1$表示。

若证明 $H_0$ 为真，则 $H_1$ 为假；若 $H_0$ 为假，则 $H_1$ 为真。

例如，设 $\bar{x}_0$ 为总体均值 $\bar{X}$ 的某一确定值。

（1）对于总体均值是否等于某一确定值的原假设可以表示为： $\begin{equation}\mathrm{H}_{0}: \quad \mathrm{X}=\overline{\mathrm{X}}_{0} \quad\left(\text { 如 } \mathrm{H}_{0}: \quad \overline{\mathrm{X}}=3190 \text { 克 }\right)\end{equation}$

其对应的备择假设则表示为： $\begin{equation}\mathrm{H}_{1}: \quad \mathrm{X} \neq \overline{\mathrm{X}}_{\mathrm{o}} \quad\left(\text { 如 } \mathrm{H}_{1}: \quad \overline{\mathrm{X}} \neq 3190\text { 克) }\right.\end{equation}$

（2）对于总体均值 $\bar{X}$ 是否大于某一确定值 $\bar{X}_0$ 的原假设可以表示为： $\begin{equation}\mathrm{H}_{\mathrm{o}}: \overline{\mathrm{X}} \geq \overline{\mathrm{X}}_{\mathrm{o}}\left(如\mathrm{H}_{\mathrm{o}}: \overline{\mathrm{X}} \geq 2000 \text { 克}\right)\end{equation}$ 其对应的备择假设则表示为：

\[\begin{equation}\mathrm{H}_{1}: \quad \overline{\mathrm{X}}<\overline{\mathrm{X}}_{\mathrm{o}} \quad\left(如\mathrm{H}_{1}: \quad \overline{\mathrm{X}}<2000 \text { 克}\right)\end{equation}\]

（3）对于总体均值 $\bar{X}$ 是否小于某一确定值 $\bar{X}_0$ 的原假设可以表示为：

\[\begin{equation}\mathrm{H}_{0}: \quad \overline{\mathrm{X}} \leq \overline{\mathrm{X}}_{0} \quad\left(如\mathrm{H}_{0}: \quad \overline{\mathrm{X}} \leq 5 \%\right)\end{equation}\]

其对应的备择假设则表示为：

\[\begin{equation}\mathrm{H}_{1}: \quad \overline{\mathrm{X}}>\overline{\mathrm{X}}_{\mathrm{o}}\left(\text { 如 } \mathrm{H}_{1}: \quad \overline{\mathrm{X}}>5 \%\right)\end{equation}\]

注意：原假设总是有等号： $=$ 或 $≤$ 或 $≥$。

双侧检验和单侧检验

根据假设的形式不同，假设检验可以分为双侧假设检验和单侧假设检验。

双侧检验与单侧检验的(假设的形式)

双侧检验：只强调差异而不强调方向性的检验称为双侧检验。

单侧检验：强调某一方向的检验称为单侧检验。又分左侧检验和右侧检验。通常适用于检验某一参数是否“大于”或 “优于”、“快于”及“小于”、“劣于”、“慢于”另一参数等一类问题。

拒绝域、接受域和临界值

在规定了检验的显著性水平 $α$ 后，根据容量为 n 的样本，按照统计量的理论概率分布规律，可以确定据以判断拒绝和接受原假设的检验统计量的临界值。

临界值将统计量的所有可能取值区间分为两互不相交的部分，即原假设的拒绝域和接受域。

接受域: 原假设为真时允许范围内的变动，应该接受原假设。

拒绝域: 当原假设为真时只有很小的概率出现，因而当统计量的结果落入这一区域便应拒绝原假设，这一区域便称作拒绝域。

假设检验的两类错误

根据假设检验做出判断无非下述四种情况：

1、原假设真实，并接受原假设，判断正确；

2、原假设不真实，且拒绝原假设，判断正确；

3、原假设真实，但拒绝原假设，判断错误；

4、原假设不真实，却接受原假设，判断错误。

假设检验是依据样本提供的信息进行判断，有犯错误的可能。所犯错误有两种类型：

第一类错误是原假设 $H_0$ 为真时，检验结果把它当成不真而拒绝了。犯这种错误的概率用 $α$ 表示，也称作 $α$ 型错误或弃真错误。
第二类错误是原假设 $H_0$不为真时，检验结果把它当成真而接受了。犯这种错误的概率用 $β$ 表示，也称作 $β$ 型错误或取伪错误。

正确决策和犯错误的概率何以归纳为下表

两类错误关系的图示

两类错误的关系

在样本容量n一定的情况下，假设检验不能同时做到犯 α 和 β 两类错误的概率都很小。若减小α错误，就会增大犯β 错误的机会；若减小β错误，也会增大犯α错误的机会。要使α和β同时变小只有增大样本容量。但样本容量增加要受人力、经费、时间等很多因素的限制，无限制增加样本容量就会使抽样调查失去意义。因此假设检验需要慎重考虑对两类错误进行控制的问题。

假设检验的步骤

概述

(一)、根据研究需要提出原假设 $H_0$ 和备择假设 $H_1$

(二)、确定适当的检验统计量

(三)、确定显著性水平 $\alpha$ 和临界值及拒绝域

(四)、根据样本数据计算检验统计量的值(或 $p$ 值)

(五)、做出决策：(两种方法)

(1)、将检验统计量的值和临界值比较，做出拒绝或接受原假设的决策。

(2)、由步骤五的检验统计量计算 $p$ 值，利用 $p$ 值确定时候拒绝原假设。

注意事项

(一)、根据研究需要提出原假设 $H_0$ 和备择假设 $H_1$

⑴对任一假设检验问题，其所有可能结果均应包括在所提出的两个对立假设中，原假设与对立假设总有一个、也只能有一个成立。

⑵原假设一定要有等号： =或 ≤ 或 ≥。原假设不是随意提出的，应该本着“不轻易拒绝原假设”的原则。

双侧检验原假设和备择假设的确定

双侧检验属于决策中的假设检验。即不论是拒绝 H0 还是接受 H0，都必需采取相应的行动措施。

例如，某某种零件的尺寸，要求其平均长度为 10厘米，大于或小于10厘米均属于不合格。待检验问题是该企业生产的零件平均长度是10厘米吗?(属于决策中的假设)则建立的原假设与备择假设应为

\[\begin{equation}H_{0}: \bar{X}=10 \quad H_{1}: \bar{X} \neq 10\end{equation}\]

单侧检验原假设和备择假设的确定

应区别不同情况采取不同的建立假设方法。

对于检验某项研究是否达到了预期效果

一般是将研究的预期效果（希望、想要证明的假设）作为备择假设H1，将认为研究结果无效作为原假设 H0。先确立备择假设H1。因为只有当检验结果与原假设有明显差别时才能拒绝原假设而接受备择假设，原假设不会轻易被拒绝，就使得希望得到的结论不会轻易被接受，从而减少结论错误。

例如：有研究预计，采用新技术生产后将会使某产品的使用寿命明显延长到1500小时以上。则建立的原假设与备择假设

\[\begin{equation}\mathrm{H}_{\mathrm{o}}: \overline{\mathrm{X}} \leq 1500 \quad \mathrm{H}_{1}: \overline{\mathrm{X}}>1500\end{equation}\]

例如，有研究预计，改进生产工艺后会使某产品的废品率降低到2%以下。则建立的原假设与备择假设应为：

\[\begin{equation}\mathrm{H}_{\mathrm{o}}: \overline{\mathrm{X}} \geq 2 \% \quad \mathrm{H}_{1}: \overline{\mathrm{X}}<2 \%\end{equation}\]

对于检验某项声明的有效性

一般可将所作的声明作为原假设。将对该声明的质疑作为备择假设。先确立原假设H0。因为除非有证据表明“声明”无效，否则就应认为该“声明”是有效的。

例如，某灯泡制造商声称，该企业生产的灯泡平均使用寿命在1000小时以上。通常除非样本能提供证据表明使用寿命在1000小时以下，否则就应认为厂商的声称是正确的。建立的原假设与备择假设应为：

\[\begin{equation}\mathrm{H}_{\mathrm{o}}: \overline{\mathrm{X}} \geq 1000 \quad \mathrm{H}_{1}: \quad \overline{\mathrm{X}}<1000\end{equation}\]

(二)、确定适当的检验统计量

假设检验根据检验内容和条件不同需要采用不同的检验统计量。

在一个正态总体的参数检验中，Z 统计量和 t 统计量常用于均值和比例的检验，χ2 统计量用于方差的检验。选择统计量需考虑的因素有被检验的参数类型、总体方差是否已知、用于检验的样本量大小等。

(三)、确定显著性水平 $\alpha$ 和临界值及拒绝域

显著性水平α是当原假设为正确时被拒绝的概率，是由研究者事先确定的。
显著性水平的大小应根据研究需要的精确度和可靠性而定。通常取α＝0.05或α＝0.01，即接受原假设的决定是正确的可能性（概率）为95％或99 ％。
根据给定的显著性水平α，查表得出相应的临界值，同时指定拒绝域。

(四)、根据样本数据计算检验统计量的值(或 $p$ 值)

(五)、做出决策

例如，总体标准差σ已知时根据样本均值计算统计量Z的公式为 $\begin{equation}Z=\frac{\bar{x}-\bar{X}}{\sigma / \sqrt{n}}\end{equation}$ 如果检验统计量的值落入拒绝域，则拒绝原假设，接受备择假设；如果检验统计量的值落入接受域，则接受原假设，拒绝备择假设。

利用 P 值进行决策

进行检验的程序可以根据检验统计量落人的区域作出是否拒绝原假设的决策。

在确定 $\alpha$ 以后，拒绝域的位置也就相应确定了，其好处是进行决策的界限清晰，但缺陷是进行决策面临的风险是笼统的。在上面的例子中，计算的 $z=2.5$，落人拒绝域，我们拒绝原假设，并知道犯弃真错误的概率(面临的风险)为0.05，如果计算的 $z=2.0$，同样落人拒绝域，我们拒绝原假设面临的风险也是0.05。0.05 是一个通用的风.险概率，这是用域表示的缺陷，但根据不同的样本结果进行决策，面临的风险事实上是有差别的，

为了精确地反映决策的风险度，可以利用P值进行决策。

为了解什么是P值，让我们回到前面的例子。

根据随机抽样测得:1990年的样本均值 $\bar{x}$=3 210 克，与1989年的总体均值 3190 克相差20克，20克的差异究竟是大还是小? 换句话说，如果原假设成立，即1990年新生儿体重的总体均值与1989年新生儿体重的总体均值相同，那么随机抽取出n= 100的样本，其均值大于3210克的概率有多大呢? 我们把这个概率称为P值，所以P值就是当原假设为真时所得到的样本观察结果或更极端结果出现的概率。如果P值很小，说明这种情况发生的概率很小，而如果出现了，根据小概率原理，我们就有理由拒绝原假设，P值越小，我们拒绝原假设的理由就越充分。

P值是通过计算得到的，P值的大小取决于三个因素，一个是样本数据与原假设之间的差异，在新生儿体重的例子里这个差异是20克;另一个是样本量，这里n=100;再一个是被假设参数的总体分布。在这个例子中计算出的P=0.012 42，这就是说，如果原假设成立，样本均值等于和大于3210克的概率只有0.012 42，这是很小的，由此我们可以拒绝原假设，得到与前面z值检验相同的结论，如图8–4所示。

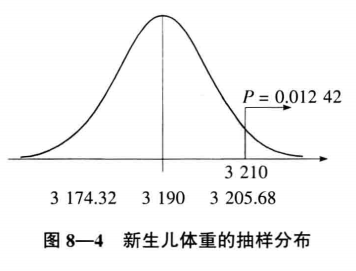
P 值的长处是它反映了观察到的实际数据与原假设之间不一-致的概率值，与传统的拒绝域范围相比，P是一个具体的值，这样就提供了更多的信息。如果事先确定了显著性水平，如 $\alpha$ =0.05，则在双侧检验中，P>0. 025( $\alpha$ /2=0.025)不能拒绝原假设; 反之，P<0. 025则拒绝原假设。在单侧检验中，P>0. 05不能拒绝原假设，P<0.05则拒绝原假设。当然，也可以直接使用 P 值进行决策，这时 P 值本身就代表了显著性水平。我们也可以使用P值，按照所需要的显著性水平进行判断和决策，具体做法就是用P值和需要的显著性水平进行比较。

例题

某批发商欲从厂家购进一批灯泡，根据合同规定灯泡的使用寿命平均不能低于1 000小时。已知灯泡燃烧寿命服从正态分布，标准差为200小时。在总体中随机抽取了100个灯泡，得知样本均值为960小时，批发商是否应该购买这批灯泡?

:这是一个单侧检验问题。显然，如果灯泡的燃烧寿命超过了1000小时，批发商是欢迎的，因为他用已定的价格(灯泡寿命为1000小时的价格)购进了更高质量的产品。因此，如果样本均值超过1000小时，他会购进这批灯泡。问题在于样本均值为960小时他是否应当购进。因为即便总体均值为1000小时，由于抽样的随机性，样本均值略小于1000小时的情况也是会经常出现的。在这种场合下，批发商更为关注可以容忍的下限，即当灯泡寿命低于什么水平时拒绝。于是检验的形式为: $\begin{equation}\begin{array}{l} H_{0}: \mu \geqslant 1000 \\ H_{1}: \mu<1000 \end{array}\end{equation}$

一个总体参数的检验

检验统计量的确定

根据假设检验的不同内容和进行检验的不同条件，需要采用不同的检验统计量，在一个总体参数的检验中，用到的检验统计量主要有三个: $z$ 统计量，$t$ 统计量，$\chi^2$ 统计量。$z$ 统计量和 $t$ 统计量常常用于均值和比例的检验，$\chi^2$ 统计量则用于方差的检验。选择什么统计量进行检验需要考虑一些因素，这些因素主要有样本量 $n$ 的大小，总体的标准差 $σ$ 是否已知。

样本量

样本量大小是选择检验统计量的一个要素。在样本量大的条件下，如果总体为正态分布，样本统计量服从正态分布;如果总体为非正态分布，样本统计量渐近服从正态分布。所以在这种情况下，我们都可以把样本统计量视为正态分布，这时可以使用 $z$ 统计量( $z$ 分布)。即在总体标准差 $σ$ 已知时，有

\[\begin{equation}z=\frac{\bar{x}-\mu_{0}}{\sigma / \sqrt{n}}\end{equation}\]

实践中当总体标准差 $σ$ 未知时，可以用样本标准差 $s$ 代替，上式可以写为:

\[\begin{equation}z=\frac{\bar{x}-\mu_{0}}{s / \sqrt{n}}\end{equation}\]

样本量较小时，情况有些复杂。在假设总体为正态分布的前提下，要看我们是否掌握总体标准差 $σ$ 的信息。

标准差 $\sigma$ 是否已知

在样本量较小的情况下，如果总体标准差已知，样本统计量服从正态分布，这时可以采用 $z$ 统计量。

如果总体标准差未知，进行检验所依赖的信息有所减少，这时只能使用样本标准差，样本统计量服从 $t$ 分布，应该采用 $t$ 统计量。与正态分布相比，$t$ 分布更为扁平，在相同概率条件下，$t$ 分布的临界点向两边更为扩展，临界点与中心距离更远，这意味着推断的精度下降，这是总体标准差 $σ$ 未知所要付出的代价。

$t$ 统计量的计算公式

\[\begin{equation}t=\frac{\bar{x}-\mu_{0}}{s / \sqrt{n}}\end{equation}\]

$t$ 统计量的自由度为 $n-1$

由上述讨论看出，样本量大小是选择检验统计量-一个很重要的因素，在大样本情况下一般可以使用 $z$ 统计量。但样本量 n 为多大才算大样本，不同的人可能给出不同的回答，同时也与被检验的对象有关。仅就分布本身而言，当 n 较小时，$t$ 分布与 $z$ 分布的差异是明显的，随着 n 的扩大，$t$ 分布向 $z$ 分布逼近，它们之间的差异逐渐缩小，t 分布以 z 分布为极限。当样本量 n>30 时， t 分布与 z 分布已经非常接近了，具备了用 z 分布取代 t 分布的理由。所以可以说，当n<30时，如果 $σ$ 未知，必须使用 $t $ 统计量; 在n>30的条件下，选择 t 统计量还是 z 统计量可以根据使用者的偏好。

总体均值和比例检验统计量的确定标准可以归结为

总体均值的检验

1、样本量大

总体方差 $\sigma^2$ 已知时, 构造 $z$ 统计量：

\[\begin{equation}z=\frac{\bar{x}-\mu_{0}}{\sigma / \sqrt{n}}\end{equation}\]

总体方差 $\sigma^2$ 未知时，构造 $z$ 统计量(样本方差代替总体方差)

$\begin{equation}z=\frac{\bar{x}-\mu_{0}}{s / \sqrt{n}}\end{equation}$ 例题：例1 某地区统考数学,假设该统考数学成绩服从正态分布,已知其总平均分为50分,标准差为12分。从该地区随机选择一个班作为样本，该班有学生50人，经计算该班平均成绩为53分，试问该班成绩与总成绩的差异是否显著。

解：

① 建立假设：$H_{0}: \mu=\mu_{0}, H_{1}: \mu \neq \mu_{0}$

② 计算统计量： $\begin{equation}\frac{\sigma_{}}{\sqrt{n}}=\frac{12}{\sqrt{50}}=\frac{12}{7.07}=1.7\end{equation}$

\[\begin{equation}z=\frac{\bar{x}-\mu_{0}}{\sigma / \sqrt{n}} =\frac{53-50}{1.7}=1.76\end{equation}\]

③判断结果: 因为1.76<1.96, 所以P>0.05

差异不显著,接受 H0 , 拒绝H1。故该班数学成绩与总平均成绩的差异不显著。

例题对某专业课在全国同类高校内进行统一测试，已知全体考生成绩服从正态分布，其总平均分为64分，总标准差为8.6分，从某高校随机抽取20份试卷，经计算得到这20份试卷的平均成绩为70分，问该校学生的平均成绩是否显著地优于全体学生的平均水平？

解：

① 建立假设：$H_{0}: \mu \leq \mu_{0}, H_{1}: \mu>\mu_{0}$

②计算统计量： $\begin{equation}\frac{\sigma_{}}{\sqrt{n}}=\frac{8.6}{\sqrt{20}}=\frac{8.6}{4.47}=1.92\end{equation}$

\[\begin{equation}z=\frac{\bar{x}-\mu_{0}}{\sigma / \sqrt{n}} =\frac{70-64}{1.92}=3.125\end{equation}\]

③查正态表（单侧）得：

当 $\alpha = 0.01$ 时，$z_{0.01}=2.33$ (此时计算的是0.01出的概率密度)

from scipy.stats import norm
norm.ppf(0.99)
# 2.3263478740408408

④判断结果:

因为 3.125>2.33 , 所以P<0.01。差异极其显著，拒绝 $H_0$。故该校学生的平均成绩极显著地优于全体学生的平均水平。

2、小样本，总体方差 $\sigma$ 已知

在样本量较小的情况下，如果总体标准差已知，样本统计量服从正态分布，这时可以采用 $z$ 统计量。

3、小样本，总体方差 $\sigma$ 未知

当总体分布为正态分布,总体方差未知时,样本平均数的抽样分布服从自由度为 $n-1$ 的 $t$分布,此时可用 $t$ 检验方法进行检验。 $\begin{equation}t=\frac{\bar{x}-\mu_{0}}{s / \sqrt{n}}\end{equation}$ 例题已知4岁正常男童平均体重为15.6公斤,从某幼儿园中随机抽取20名4岁男童,经测量计算出这20名男童平均体重为16 公斤,标准差为1.76公斤,试问该幼儿园4岁男童的体重与4岁正常男童平均体重有无显著性差异?

解:

① 建立假设：$H_{0}: \mu=\mu_{0}, H_{1}: \mu \neq \mu_{0}$

② 计算统计量： $\begin{equation}\frac{s{}}{\sqrt{n-1}}=\frac{1.76}{\sqrt{20-1}}=0.4\end{equation}$

\[\begin{equation}t=\frac{\bar{x}-\mu_{0}}{s / \sqrt{n}}=\frac{16-15.6}{0.4}=1\end{equation}\]

③ 判断结果：

当 $\alpha =0.05$ 时， $df=20-1=19$

$t_{(19)0.05/2}=2.093$

因为1<2.093,所以, P>0.05，差异不显著。故该幼儿园4岁男童平均体重与正常男童平均体重无显著差异。

总体比例的检验

如果一个事件只可能有两种结果，我们将其称为二项分布，可以证明，在样本量大的情况下，若 $np>5,nq>5$ ,则可以把二项分布问题变换为正态分布问题近似地去求解。这就是说，在总体比例的检验中，通常采用 $z$ 统计量。般而言，在有关比例的问题的调查中往往使用大样本量，而小样本量的结果是极不稳定的。例如，随机抽取10个人，如果支持者有4人，支持率为40%;如果支持者有5人，支持率则为50%，样本中一个人的态度差异导致调查结果相差10个百分点，这种不稳定性是我们不愿意看到的。

在比例问题的检验中，$z$ 统计量的计算公式为:

\[\begin{equation}z=\frac{p-\pi_{0}}{\sqrt{\frac{\pi_{0}\left(1-\pi_{0}\right)}{n}}}\end{equation}\]

其中， $p$ 为样本比例；$\pi_0$ 为总体比例$\pi$ 的假设值。

总体方差的检验

单总体方差的差异检验也称为样本方差与总体方差的差异显著性检验。

对方差进行检验的程序，与均值检验、比例检验是一样的，它们之间的主要区别是所使用的检验统计量不同。方差检验所使用的是 $\chi^2$计量。对一个方差为 $\sigma^2$的正态总体反复抽样，计算每一个样本方差 $s^2$，则$s^2$的分布大体如图

由于 $s^{2}=\frac{\sum\left(x_{i}-\bar{x}\right)^{2}}{n-1}$ , 故

\[\begin{equation}\sum\left(x_{i}-\bar{x}\right)^{2}=(n-1) s^{2}\end{equation}\]

可以证明， $\sum\left(x_{i}-\bar{x}\right)^{2}$ 除以总体方差 $\sigma^{2}$ 将服从 $\chi^{2}$ 分布，即

\[\begin{equation}\chi^{2}=\frac{(n-1) s^{2}}{\sigma^{2}}\end{equation}\]

两个总体参数的检验

在许多情况下,人们需要比较两个总体的参数,看它们是否有显著的区别。例如，在相同年龄组中,高学历和低学历的职工收人是否有明显的差异;同一种教学方法.在不同的年级或不同内容的课程中是否会有不同的效果，等等。对此,可以利用两个总体参数的检验寻找答案。

检验统计量的确定

两个总体参数检验的主要内容有:两个总体均值之差的检验，两个总体比例之差的检验，两个总体方差比的检验。与一个总体参数的检验讨论的问题类似,两个总体参数的检验也涉及检验统计量的选择问题。选择什么检验统计量取决于被检验参数的抽样分布,而抽样分布与样本量大小，与总体方差 $\sigma^2 $ 是否已知都有关系。

两个总体均值之差的检验中,可能出现的情况有:

可以归纳为

两个总体均值之差的检验

1、$\sigma_{1}^{2}, \sigma_{2}^{2}$已知

两平均数之差的标准差

当两个变量间的相关系数为r时，两变量的方差为：

\[\begin{equation}\sigma_{(X-Y)}^{2}=\sigma_{X}^{2}+\sigma_{Y}^{2}-2 r \sigma_{x} \sigma_{y}\end{equation}\]

当两个变量相互独立时，其和（或差）的方差等于各自方差的和：

\[\begin{equation}\sigma_{(X \pm Y)}^{2}=\sigma_{X}^{2}+\sigma_{Y}^{2}\end{equation}\]

因此有：

\[\begin{equation}S E_{D_{\bar{X}}}=\sqrt{S E_{1}^{2}+S E_{2}^{2}}=\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}-2 r \frac{\sigma_{1}}{\sqrt{n_{1}}} \frac{\sigma_{2}}{\sqrt{n_{2}}}}\end{equation}\]

当两个样本独立时，r=0，这时上述公式为

\[\begin{equation}S E_{D_{\bar{X}}}=\sqrt{S E_{1}^{2}+S E_{2}^{2}}=\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}\end{equation}\]

例题