一、P-value(P值)
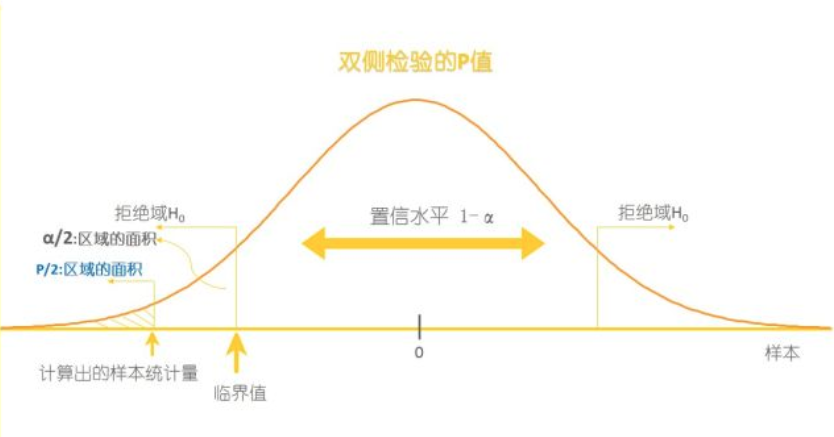
P-value 的定义就是 “The probability computed assuming $H_0$ is true, that the statistic would have a value as extreme or more than the one observed in the sample”
P值( P-Value,Probability,Pr)
就是默认 $H_0$ 是对的, 然后给定某个数,跟这个数一样极端或者比它还极端的概率就是 P-value。(大白话就是这个数都这么远了概率这么低这么离谱,比它更偏远的数更离谱,那 $H_0$ 就不可能对呀,这种时候否定 $H_0$ )
做题的话, 就比如说我们知道某学校的学生每个人平均考78分,然后 $H_0$ 就是平均考78分。实际抽了几十个学生调查出来这几十个平均考70分,问最多70分时候这个可能性(P-value)是多少,可能性低不低,能不能否定这个 $H_0$(学校里所有学生平均78分,population mean=78)的假设。
那什么东西来决定这个p-value够不够低呢?
这时候我们需要一条水位线—Significant Level(显著性水平),用 $α$ 表示
什么是P值:被称为观察到的(或实测的)显著性水平。反映实际观测到的数据与原假设 $H_0$ 之间不一致的程度。
二、α(Significant Level,显著性水平)
得到 P-value 之后要看它在不在 significant level 里,通常是用 α 表示。
你可以自己决定α是多少。
P-value越小就越能否定 $H_0$ ** 。 如果 P-value 落在 α 之内了(P-value小于等于α)那就说明 **H0是错的 。(是不是真的错了另说,也可能说是 $H_ 0 $ 错了但其实它对了,也就是Type I Error,这个在此不深入探讨)
低于significant level这个水位线(P-value小于等于α)的话就可以否定 $H_0$ ,高于这个线的话就是否定不了 $H_0$ 。前面说了你可以自己决定,相当于你自己可以决定这个水位线标哪儿。
如果这个水位线设置得高了呢, 比如 α=0.01 和 α=0.1 的时候:如果 P-value 是0.02, 那么当 α=0.01就不可以否定 H0,因为 0.02>0.01 当 α=0.1的时候就可以否定 H0,因为 0.02<0.1
所以说Significant level高了的话就更可能否定 $H_0$ 。
p值和显著性水平 $\alpha$ 根本不是一回事,很多人包括提问者把它们混为-谈了。 $\alpha$ 是人为定的,取0.1、0.05、0.01随你需要, 当然也不能瞎选。 $\alpha$ 定了, 拒绝域也就确定了。接下来才要看抽样的结果, p 值是根据样本算出来的,不是人为确定的。要注意拒绝原假设的条件是p值小于 $\alpha$ 。如果 $\alpha$ 越大,则拒绝的可能性越大,但不是 $\alpha$ 值变大了,p值还是那个p值,除非你重新抽样。举个例子,如果计算出来的p值是0.02, $\alpha$ 选0.05的时候可以拒绝原假设,如果选0.01 就无法拒绝了。所以把 $\alpha$ 与p值分开看就清楚了。
三、置信水平
$1-\alpha$
四、怎么算p值?
取决于是不同的分布(distribution)
五、二者之间的关系
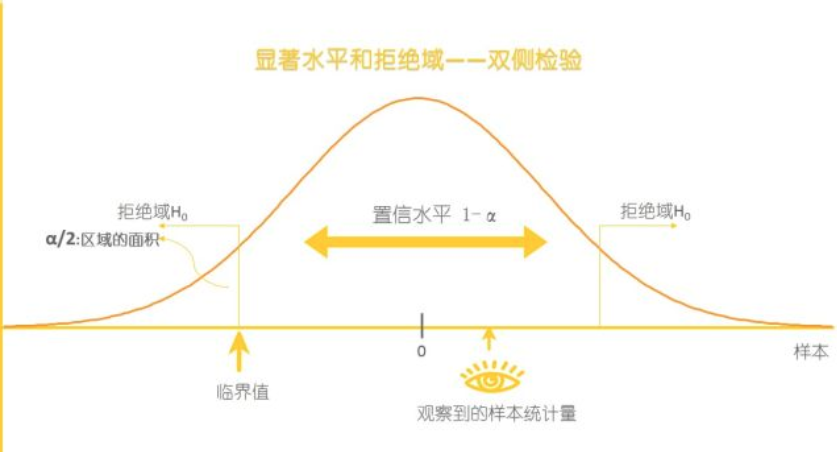

决策规则:
1.给定显著性水平,查表得出相应的的临界值。
2.利用样本数据,计算检验统计量的值与显著性水平的临界值进行比较。(也可以通过P值与显著性水平的临界值比较)
3.作出决策
-双侧检验:|统计量|>临界值,拒绝H0
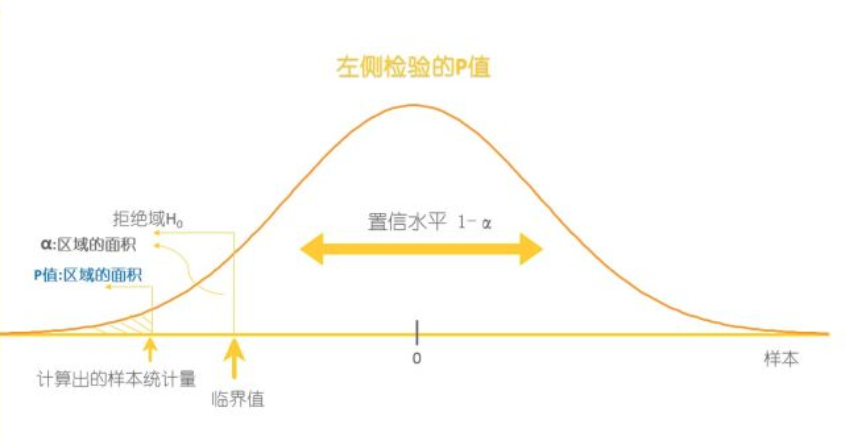
-左侧检验:统计量<-临界值,拒绝H0
-右侧检验:统计量>临界值,拒绝H0
P值就是计算出的样本统计量的面积,当 $P<α$ 时,就拒绝 $H_0$ 。