分类数据分析
在上一章中介绍了两个体比例之差的检验, 如果对更多的总体比例进行比较, 则需要采用本章介绍的方法。对分类数据进行分析的统计方法主要是利用 $\chi^2$ 分布,许多教材又将其称为 $\chi^2$ 检验。 $\chi^2$ 检验的应用主要表现在两个方面: 拟合优度检验和独立性检验。列联表是进行独性检验的重要工具。
分类数据
分类数据是对事物进行分类的结果,其特征是,调查结果虽然用数值表示,但不同数值描述了调查对象的不同特征。例如,研究青少年家庭状况与行为之间的关系,青少年家庭状况是一个分类数据,可以分为“完整家庭”和“离异家庭”,如果调查结果为“1”,则表示被调查者来自完整家庭,调查结果为“2”, 则表示被调查者来自离异家庭。青少年行为也可以分为两类,“犯罪”和“未犯罪”,分别用 “1” 和 “2” 表示。对这类题是在汇总数据的基础上进行分析的,数据汇总的结果表现为频数。
由上述内容可知,分类数据的结果是频数, $\chi^2$ 检验是对分类数据的频数进行分析的统计方法。
卡方统计量
$\chi^2$ 可以用于测定两个分类变量之间的相关程度。若用 $f_o$ 表示观察值频数(observed frequency),用$f_e$,表示期望值频数(expected frequency), 则 $\chi^2$ 统计量可以写为:
\[\begin{equation}\chi^{2}=\sum \frac{\left(f_{o}-f_{e}\right)^{2}}{f_{e}}\tag{9.1}\end{equation}\]$\chi^2$ 统计量有如下特征:
- $\chi^2$ ≥0,因为它是对平方结果的汇总
- $\chi^2$ 统计量的分布与自由度有关
- $\chi^2$ 统计量描述了观察值与期望值的接近程度。
两者越接近,即 $f_o -f_e$ 的绝对值越小,计算出的 $\chi^2$ 值就越小; 反之, $f_o -f_e$ 的绝对值越大, 大,计算出的 $\chi^2$ 值也越大。 $\chi^2$ 检验正是通过对 $\chi^2$ 的计算结果与 $\chi^2$ 分布中的临界值进行比较,做出是否拒绝原假设的统计决策。
$\chi^2$ 分布与自由度的关系

自由度越小, 分布就越向左倾斜,随着自由度的增加, $\chi^2$ 分布的倾斜程度趋于缓解, 逐渐显露出对称性, 随着自由度继续增大,卡方分布将趋于对称的正态分布。
利用 $\chi^2$ 分布,可以对分类数据进行拟合优度检验和独立性检验
拟合优度检验
拟合优度检验(goodnessoffittest) 是用 $\chi^2$ 统计量进行统计显著性检验的重要内容之一。它是依据总体分布状况,计算出分类变量中各类别的期望频数,与分布的观察频数进行对比,判断期望频数与观察频数是否有显著差异,从而达到对分类变量进行分析的目的。
例如,在泰坦尼克号的例子中,我们关注在这次海难中,幸存者的性别是否有显著差异。当时船上共有2 208人,其中男性1 738 人,女性470人。海难发生后,幸存者共718人,其中男性374人,女性344人。海难后存活比率为 $718/2 208=0. 325$。如果是否活下来与性别没有关系,那么按照这个比率,在1 738位男性中应该存活 $17380. 325=565$人,在470位女性中应该存活 $470 0.325=153$人。565和153就是期望频数,而实际存活结果就是观察频数。通过期望频数和观察频数的比较,能够从统计角度做出存活与性别是否有关的判断。

对总体比例的检验,也可以采用拟合优度的方法。
例如

采用拟合优度的方法。

列联分析:独立性检验
拟合优度检验是对一个分类变量的检验,有时我们会遇到两个分类变量的问题,看这两个分类变量是否存在联系。例如原料有不同的等级,原料又产自不同的地区。原料等级和原料生产地就是两个分类变量。我们关心这两者是否有关联,是不是某些地区生产的原料有更好的质量。对于两个分类变量的分析,称为独立性检验,分析过程可以通过列联表的方式呈现,故有人把这种分析称为列联分析。
列联表
列联表(contingency table) 是由两个以上的变量进行交叉分类的频数分布表。
例如欲分析原料的质量是否与生产地有关,将500件随机抽取的产品按质量和产地构造列联表如下
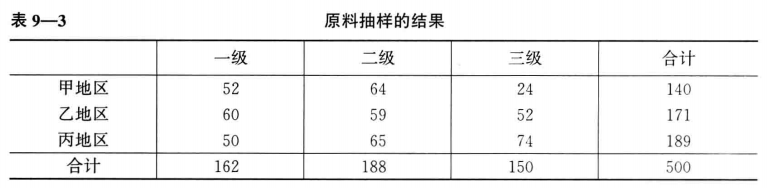
表中的行(row)是产地变量,这里划分为三类:甲、乙、丙三个地区。表中的列(column)是产品等级变量,这里也划分为三类:一级品、二级品、三级品。因此,表9-3是一个 3X3 列联表,表中的每个数据都反映了产地和产品等级两个方面的信息。由于列联表中的每个变量都可以有两个或两个以上的类别,列联表会有多种形式。不妨将横向变量(行)的划分类别视为R, 纵向变量(列)的划分类别视为C,则可以把每一个具体的列联表称为 RXC 列联表,如我们把表9- 3 称为 3X3 列联表。
列联表的基本形式
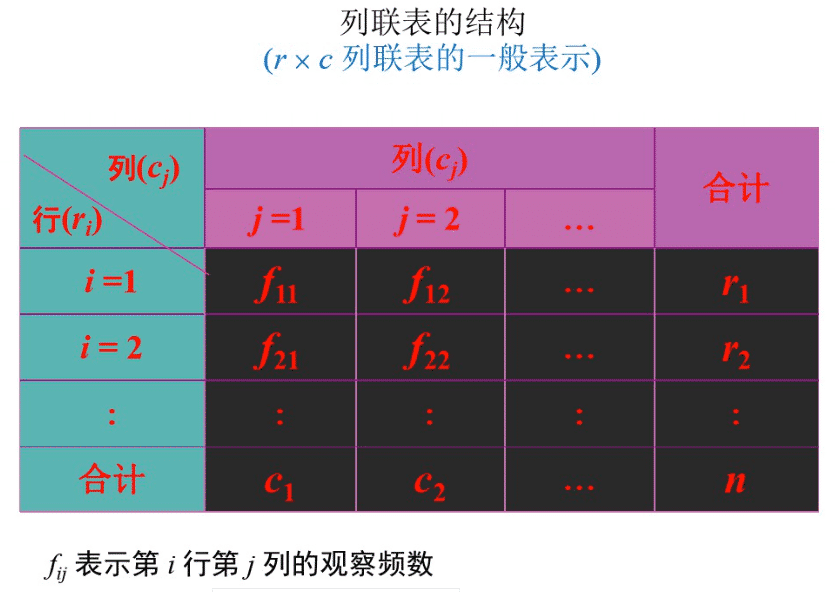
有两个以上的变量交叉分类的频数分布表
行变量的类别用 $r$ 表示,$r_i$ 表示第 $i$ 个类别
列变量的类别用 $c$ 表示,$c_j$ 表示第 $j$ 个类别
每种组合的观察频数用 $f_{ij}$表示
表中列出了行变量和列变量的所有可能的组合,所以称为列联表
一个 $r$ 行 $c$ 列的列联表称为 rxc 列联表
独立性检验
独立性检验就是分析列联表中行变量和列变量是否相互独立,在表9-3中,也就是检验各个地区和原料质量之间是否存在依赖关系。
例题
一种原料来自三个不同的地区,原料质量被分成三个不同等级。从这批原料中随机抽取500件进行检验,结果如表9-3所示,要求检验各个地区和原料质量之间是否存在依赖关系( $\alpha$ =0. 05)?
解:
$H_{0}:$ 地区和原料等级之间是独立的(不存在依赖关系) $H_{1}:$ 地区和原料等级之间不独立(存在依赖关系)
这里分析的关键是获得期望值。
在第一行,甲地区的合计为140,用 $140/500$ 作为甲地区原料比例的估计值。
在第一列,一级原料的合计为162,用 $162/500$ 作为一级原料比例的估计值。如果地区和原料等级之间是独立的,则可以用下面的公式估计第一个单元(甲地区,一级)中的期望比例:
令 : $A$ = 样本单位来自甲地区的时间
$B$ = 样本单位属于一级原料的事件
根据独立性的概率乘法公式,有
\[\begin{equation}\begin{aligned} P(\text { 第一单元 }) &=P(A B) \\ &=P(A) P(B) \\ &=\left(\frac{140}{500}\right)\left(\frac{162}{500}\right) \\ &=0.09072 \end{aligned}\end{equation}\]0.09072 是第一个单元中的期望比例,其相应的频数期望值为:
\[0.09072* 500=45.36\]一般地,可以采用下式计算任何一个单元中频数的期望值:
\[\begin{equation}f_{e}=\frac{R T}{n} \times \frac{C T}{n} \times n=\frac{R T \times C T}{n}\tag{9.3}\end{equation}\]式中 $f_e$ 为给定单元格中的频数期望值, $RT$ 为给定单元格所在行的合计;$CT$ 为给定单元格所在列的合计;$n$ 为观察值的总个数,即样本量。
根据表 9-3 和上式,计算结果如表 9-4 所示。

列联表的相关测量
前面讨论了利用 $\chi^2$ 分布对两个分类变量之间的相关性进行统计检验。如果变量相互独立,说明它们之间没有联系;反之,则认为它们之间存在联系。接下来的问题是,如果变量之间存在联系,它们之间的相关程度有多大? 这一节主要讨论这个问题。
对两个变量之间相关程度的测定,主要用相关系数表示。正如前面所言,列联表中的变量通常是类别变量,它们所表现的是研究对象的不同品质类别。所以,可以把这种分类数据之间的相关称为品质相关。经常用到的品质相关系数有以下几种。
$\varphi$ 相关系数
$\varphi$ 相关系数 ($\varphi$ $correlation coefficient$) 是描述 2X2 列联表数据相关程度最常用的一种相关系数。它的计算公式为:
\[\begin{equation}\varphi=\sqrt{\chi^{2} / n}\tag{9.4}\end{equation}\]式中, $\chi^2$ 是按 \(\chi^{2}=\sum \frac{\left(f_{o}-f_{e}\right)^{2}}{f_{e}}\) 计算得到的;$n$ 为列联表中的总频数,也即是样本量。
说 $\varphi$ 系数适合 2x2 列联表,是因为对于 2x2 的列联表中的数据,计算出的 $\varphi$ 系数可以控制在 $0\sim 1$ 这个范围。表 9-8 是一个简单的 2x2 的列联表。

表中 $a,b,c,d$ 均为条件频数,当 $X,Y$ 相互独立,不存在相关关系时,频数应有下面的关系:
\[\begin{equation}\frac{a}{a+c}=\frac{b}{b+d}\end{equation}\]化简后有: \(ad=bc\)
因此,差值 $ad -bc$ 的大小可以反映变量之间相关程度的高低。差值越大,说明两个变量的相关程度越高。$\varphi$ 系数就是以 $ad - bc$的差值为基础,对两个变量相关程度的测定。
由式 (9.3) 知,在 2x2 的列联表中,每个单元格中频数的期望值为:
\[\begin{equation}\begin{array}{l} e_{11}=\frac{(a+b)(a+c)}{n} \\ e_{21}=\frac{(a+c)(c+d)}{n} \\ e_{12}=\frac{(a+b)(b+d)}{n} \\ e_{22}=\frac{(b+d)(c+d)}{n} \end{array}\end{equation}\]由式 (9.1) 知
\[\begin{equation}\begin{aligned} \chi^{2} &=\frac{\left(a-e_{11}\right)^{2}}{e_{11}}+\frac{\left(b-e_{12}\right)^{2}}{e_{12}}+\frac{\left(c-e_{21}\right)^{2}}{e_{21}}+\frac{\left(d-e_{22}\right)^{2}}{e_{22}} \\ &=\frac{n(a d-b c)^{2}}{(a+b)(c+d)(a+c)(b+d)} \end{aligned}\end{equation}\]将此结果带入式(9.4) 得到
\[\begin{equation}\varphi=\sqrt{\frac{\chi^{2}}{n}}=\frac{a d-b c}{\sqrt{(a+b)(c+d)(a+c)(b+d)}}\tag{9.5}\end{equation}\]
列联相关系数
列联相关系数又称列联系数(coefficient of contingency), 简称 $c$ 系数,主要用于大于 2X2 列联表的情况。c系数的计算公式为:
\[\begin{equation}c=\sqrt{\frac{\chi^{2}}{\chi^{2}+n}}\tag{9.6}\end{equation}\]当列联表中的两个变量相互独立时,系数 $c=0$,但它不可能大于1,这一点从式(9.6)中也可以反映出来。$c$ 系数的特点是,其可能的最大值依赖于列联表的行数和列数,且随着 R 和 C 的增大而增大。
例如,当两个变量完全相关时,对于2X2表,$c$=0.707 1; 对于3X3表,$c$ = 0.8165; 而对于4X4表,$c$ = 0.87。因此,根据不同的行和列计算的列联系数不便于比较,除非两个列联表中行数和列数一致。这是列联系数的局限性。但由于其计算简便,且对总体的分布没有任何要求,所以列联系数仍不失为一种适应性较广的测度值。
$V$ 相关系数

数值分析

列联分析中应注意的问题
卡方分布的期望值准则
前面谈到的用 $\chi^2$ 分布进行独立性检验,要求样本量必须足够大,特别是每个单元中的期望频数(理论频数)不能过小,否则应用 $\chi^2$ 检验可能会得出错误结论。关于小单元的频数通常有两条准则: 一条准则是,如果只有两个单元,每个单元的期望频数必须是5或5以上,如表9–16 所示。

此时有两个单元,或分为两个类别: 患过肝炎和未患过肝炎。样本量足够大,每个单元的期望频数 $f_e≥5$,因此可以使用 $\chi^2$ 检验。
另一条准则是,倘若有两个以上的单元,如果20%的单元期望频数 $f_e$ 小于5,则不能应用 $\chi^2$ 检验。
根据这个准则,表 9- 17 中的数据可以计算 $\chi^2$ ,因为 6 个单元中只有 1 个单元的期望频数小于5。而表9- 18中的数据不能应用$\chi^2$ 检验,因为7个单元中有 3 个单元的期望频数小于5。