利用 scipy.stats 中的 ttest_1samp, ttest_ind, ttest_rel 实现 T 检验。
ttest_rel 案例分析。
引入所需的包
from scipy import stats
import numpy as np
注:ttest_1samp, ttest_ind, ttest_rel均进行双侧检验
单样本T检验-ttest_1samp
目的:检验单样本的均值是否和已知总体的均值相等(均值已知)。
scipy.stats.ttest_1samp(a, popmean, axis=0, nan_policy='propagate')
ttest_1samp:单独样本 t 检验,
返回的第1个值 t 是假设检验计算出的( t 值),
第2个值 p 是双尾检验的 p 值
生成50行 $*$ 2列的数据
np.random.seed(1) # 保证每次运行都会得到相同结果
# 均值为5,方差为10
rvs = stats.norm.rvs(loc=5, scale=10, size=(50))
stats.ttest_1samp(rvs, popmean=1)
结果:
Ttest_1sampResult(statistic=4.507936852278188, pvalue=4.083376388334293e-05)
# 均值为5,方差为10
rvs = stats.norm.rvs(loc=5, scale=10, size=(50,2))
#检验两列数的均值与1和2的差异是否显著
stats.ttest_1samp(rvs, [1, 2])
结果:
Ttest_1sampResult(statistic=array([4.63604301, 2.09629777]), pvalue=array([2.66146644e-05, 4.12421515e-02]))
两独立样本t检验-ttest_ind
scipy.stats.ttest_ind
目的:检验两独立样本的均值是否相等。
生成数据
方差齐时
np.random.seed(12345678)
#loc:平均值 scale:方差
rvs1 = stats.norm.rvs(loc=5,scale=10,size=500)
rvs2 = stats.norm.rvs(loc=5,scale=10,size=500)
当两总体方差相等时,即具有“方差齐性”,可以直接检验
stats.ttest_ind(rvs1,rvs2)
结果:
Ttest_indResult(statistic=0.26833823296238857, pvalue=0.788494433695651)
当不确定两总体方差是否相等时,应先利用 levene检验,检验两总体是否具有方差齐性。
stats.levene(rvs1, rvs2)
结果:
LeveneResult(statistic=0.9775501222315258, pvalue=0.323044034693146)
p值远大于0.05,认为两总体具有方差齐性。
如果两总体不具有方差齐性,需要将 equal_val 参数设定为“False”。
需注意的情况:
如果两总体具有方差齐性,错将 equal_var设为False,p值变大
stats.ttest_ind(rvs1,rvs2, equal_var = False)
结果:
Ttest_indResult(statistic=0.26833823296238857, pvalue=0.7884945274950106)
两总体方差不等时,若没有将equal_var参数设定为False,则函数会默认equal_var为True,这样会低估p值
rvs3 = stats.norm.rvs(loc=5, scale=20, size=500)
stats.ttest_ind(rvs1, rvs3, equal_var = False)
结果:
Ttest_indResult(statistic=-0.46580283298287956, pvalue=0.6414964624656874)
stats.ttest_ind(rvs1, rvs3)
结果:
Ttest_indResult(statistic=-0.46580283298287956, pvalue=0.6414582741343561)
当方差不齐 且计算的时候需要用到自由度的时候,此方法不合适 ,此时可以用到 statsmodels.stats.weightstats.ttest_ind
方差不齐时
上述分析可见 Scipy 的双独立样本t检验不能返回自由度,对于后面计算置信区间不方便。所以我们使用另一个统计包(statsmodels)
双独立(independent)样本t检验
statsmodels.stats.weightstats.ttest_ind
import statsmodels.stats.weightstats as st
'''
ttest_ind:独立双样本t检验,
usevar='unequal'两个总体方差不一样
返回值
第1个值t是假设检验计算出的(t值),
第2个p_two是双尾检验的p值
第3个df是独立双样本的自由度
'''
t,p_two,df=st.ttest_ind(data['A'],data['B'],
usevar='unequal')
statsmodels.stats.weightstats.ttest_ind(x1, x2, alternative=’two-sided’, usevar=’pooled’, weights=None, None, value=0)
- usevarstr, ‘pooled’ or ‘unequal’If pooled, then the standard deviation of the samples is assumed to be the same. If unequal, then Welsh ttest with Satterthwait degrees of freedom is used
配对样本T检验(ttest_rel)
用于分析配对定量数据之间的差异对比关系。与独立样本t检验相比,配对样本T检验要求样本是配对的。两个样本的样本量要相同;样本先后的顺序是一一对应的。
使用 ttest_rel()函数可以进行配对样本T检验。
# 不拒绝原假设,认为rvs1 与 rvs2 所代表的总体均值相等
np.random.seed(12345678)
rvs1 = stats.norm.rvs(loc=5,scale=10,size=500)
rvs2 = (stats.norm.rvs(loc=5,scale=10,size=500) + stats.norm.rvs(scale=0.2,size=500))
stats.ttest_rel(rvs1,rvs2)
结果:
Ttest_relResult(statistic=0.24101764965300979, pvalue=0.8096404344581155)
# 拒绝原假设,认为rvs1 与 rvs3所代表的总体均值不相等
rvs3 = (stats.norm.rvs(loc=8,scale=10,size=500) + stats.norm.rvs(scale=0.2,size=500))
stats.ttest_rel(rvs1,rvs3)
结果:
Ttest_relResult(statistic=-3.9995108708727924, pvalue=7.308240219166128e-05)
案例
相关配对检验
普鲁特效应是著名的心理学现象,展示了人们对事物的认知过程已是一个自动化的历程。当有一个新的刺激出现时,如果它的特征和原先的刺激相似或符合一致,便会加速人们的认知;反之,若新的刺激特征与原先的刺激不相同,则会干扰人们的认知,是人们所需的反应数据变长。 简单来说,普鲁特效应是当有与原有认知不同的情况下,人们的反应时间会较长。
一、描述统计分析
#导入包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
'''
路径和文件名中不要用中文,不然会报错
encoding用于指定文件的编码,因为读取的csv中有中文,所以指定文件编码为中文编码“GBK”
'''
data=pd.read_csv('E:\\data.csv',
encoding='GBK')
data.()
""
Congruent Incongruent
0 12.079 19.278
1 16.791 18.741
2 9.564 21.214
3 8.630 15.687
4 14.669 22.803
""
data.describe()
"""
Congruent Incongruent
count 24.000000 24.000000
mean 13.926875 22.350750
std 3.540219 5.010218
min 8.630000 15.687000
25% 11.895250 18.716750
50% 13.627500 21.046000
75% 15.671250 24.536000
max 22.328000 35.255000
"""
'''
第一组数据:字体内容个字体颜色一致情况下,实验者反应时间
'''
#第一组数据均值
cn_mean=data['Congruent'].mean()
#第一组数据标准差
cn_std=data['Congruent'].std()
'''
第二组数据:字体内容和颜色一致的情况下,实验者的反应时间
'''
#第二组数据均值
incn_mean=data['Incongruent'].mean()
#第二组数据标准差
incn_std=data['Incongruent'].std()
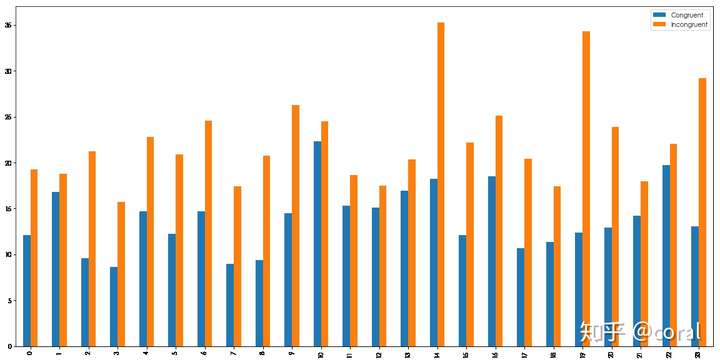
使用柱状图对两个样本数据进行对比
#两个样本数据及对比
#画板
fg=plt.figure(figsize=(20,10))
#画纸
ax=fg.add_subplot(1,1,1)
#绘制柱状图
data.plot(kind='bar',ax=ax)
#显示图形
plt.show()
print('描述统计分析结果:')
print('第一组数据:字体内容和字体颜色一致的情况下,实验者的平均反应时间是:',cn_mean,'标准差是:',cn_std)
print('第二组数据:字体内容和字体颜色不一致的情况下,实验者的平均反应时间是:',incn_mean,'标准差是:',incn_std)
print('"不一致"的情况下所用的时间均大于“一致”所用的时间,也就是当字体内容盒子体验证不一致时,实验者的反应时间变长')
二、推论统计分析
1、假设检验
1. 问题是什么?
自变量指原因。因变量是结果,自变量发生变化导致因变量改变。
自变量:实验颜色与文字是否相同
因变量:实验者反应时间
所以,我们要考察自变量两种情况对因变量的影响。
零假设和备选假设
假设第一组“一致”均值为 u1,第二组“不一致”均值为 u2
零假设 H0:人们反应时间不会因字体内容和颜色是否相同而改变(u1=u2)
备选假设H1:特鲁普效应确实存在。(u1<u2)
2、检验类型’:相关配对检验
'''
获取差值数据集,也就是“一致”这一列数据,对应减去“不一致”这一列数据
'''
#差值数据集
data['差值']=data['Congruent']-data['Incongruent']
data.head()
"""
Congruent Incongruent 差值
0 12.079 19.278 -7.199
1 16.791 18.741 -1.950
2 9.564 21.214 -11.650
3 8.630 15.687 -7.057
4 14.669 22.803 -8.134
"""
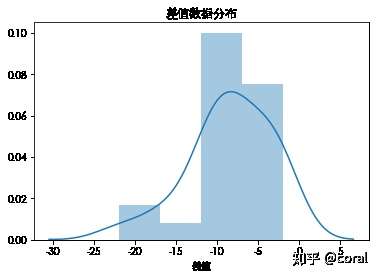
抽样分布
import seaborn as sns
sns.distplot(data['差值'])
plt.title('差值数据分布')
plt.show()
检验方向
备选假设:特鲁普效应存在,u1<u2,为避免估值过小,左尾验证
显著水平5%,t检验自由度df=n-1=25-1=24
证据是什么?
在零假设成立前提下,样本平均值概率p是多少?
from scipy import stats
t,p_twotail=stats.ttest_rel(data['Congruent'],data['Incongruent'])
print('t=',t,'双尾检验p值=',p_twotail)
结果:
t= -8.08861087281 双尾检验p值= 3.54871914972e-08
#单尾检验p值
p_onetail=p_twotail/2
print('单尾检验p值=',p_onetail)
单尾检验p值= 1.77435957486e-08
3.判断标准是什么?
#显著水平使用alpha=5%
alpha=0.05
4.做出结论
#决策
if t<0 and p_onetail<alpha:
print('拒绝零假设,特里普效应存在')
else:
print('接受零假设,特鲁普效应不存在')
结果:
拒绝零假设,特里普效应存在
假设检验报告
相关配对检验t(24)=-8.08,p=1.77e-08(α=5%),左尾检验 统计上存在显著差异,拒绝零假设,从而验证斯特鲁普效应存在。
5.置信区间
'''
1)置信水平对应的t值(t_ci)
查t表格可以得到,95%的置信水平对应的t值=2.262
2)计算上下限
置信区间上限a=样本平均值 - t_ci ×标准误差
置信区间下限b=样本平均值 - t_ci ×标准误差
'''
'''
95%的置信水平,自由度是n-1对应的t值
查找t表格获取,
也可以通过这个工具获取:https://www.graphpad.com/quickcalcs/statratio1/(利用这个工具获取t值,需要注意输入的概率值是1-95%=0.05)
'''
t_ci=2.063
#差值数据集平均值
sample_mean=data['差值'].mean()
#差值数据集标准差
sample_std=data['差值'].std()
se=stats.sem(data['差值'])
#置信水平
a=sample_mean-t_ci*se #上限
b=sample_mean+t_ci*se #下限
print('两个平均值差值的置信区间,95置信水平CI=[%f,%f]'%(a,b))
两个平均值差值的置信区间,95置信水平CI=[-10.572384,-6.275366]
6.效应量
#差值数据集对应的总体平均值为0
pop_mean=0
#差值数据集的标准差
sample_std=data['差值'].std()
d=(sample_mean-pop_mean)/sample_std
print("d=",d)
d= -1.6510807805255563
三、数据分析报告总结
1、描述统计分析
第一组样本数据:字体内容和字体颜色一致情况下,平均反应时间是: 13.89 秒,标准差是 3.47 秒
第二组样本数据:字体内容和字体颜色不一致情况下,平均反应时间是: 22.62 秒,标准差是 5.09 秒
“不一致”情况下所用时间均大于“一致”情况,也就是当字体内容和字体验证不一致时,实验者的平均反应时间变长
2、推论统计分析
1)假设检验
相关配对检验t(24)=–8.08,p=1.77e-08 (α=5%),左尾检验
统计上存在显著差异,拒绝零假设,从而验证斯特鲁普效应存在。
2)置信区间
两个平均值差值的置信区间,95%置信水平 CI=[-10.57,-6.57]
3)效应量
d= - 1.65