基于 T 检验的 AB 测试。 双侧 T 检验,方差未知。

一、实验设计
有两款键盘布局不一样的手机(A版本,B版本),你作为公司的产品经理,想在正式发布产品之前知道,哪个键盘布局对用户体验更好。
首先,我们需要设置目标,用来衡量各个版本的优劣,如果是电商网站,目标可以是点击率,注册率,页面停留时间等。
在这个键盘布局案例里,如果一个键盘布局在用户打字时拼错的概率小,那这个布局就是符合用户体验习惯的。
所以我们将目标定为不同布局的打错字数。
有了目标以后,下一步就是采集数据。
通过随机抽取实验者,将实验者分成2组,每组25人,A组使用键盘布局A,B组使用键盘布局B。让他们在30秒内打出标准的20个单词文字消息,然后记录打错字的数量。
我们将数据记录在Excel中,A列是使用键盘A打错字的数量,B列是使用键盘B打错字的数量。
二、描述统计分析
进行统计分析时,第一步必须先计算出描述统计分析的特征,以便后期进一步分析结果。
导入模块
from warnings import simplefilter
simplefilter(action='ignore',category=FutureWarning)
import pandas as pd
import numpy as npm
import matplotlib.pyplot as plt
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False
导入数据集
data = pd.read_excel('键盘AB测试.xlsx')
data.head()
"""
A B
0 6 6
1 6 11
2 2 8
3 7 5
4 8 11
"""
计算A、B两组数据的平均出错数和方差
# 第一组数据:A键盘的平均出错数和方差
A_mean = data['A'].mean()
A_std = data['A'].std()
第二组数据:B键盘的平均出错数和方差
# 第二组数据均值
B_mean = data['B'].mean()
# 第二组数据标准差
B_std = data['B'].std()
可以用data.describe()直接看出来的, 但是不方便后面调用
使用柱状图进行数据比较
data.plot(kind='bar')

结合上述计算结果,可以初步看出:
第一组数据:A键盘,实验者的打字平均出错数是: 5.08 个,标准差是 2.05993527406405 个
第二组数据:B键盘,实验者的打字平均出错数是: 7.8 个,标准差是 2.6457513110645903 个
可见,A键盘的出错均值小于B键盘
三、推论统计分析
推论统计分析报告中包括:假设检验,置信区间,效应量
1.问题是什么?
零假设和备选假设
本次统计主要是为了确定A,B两种键盘的出错率,因此作出以下假设
零假设 H0:A, B两种键盘打字出错率没有明显区别;
备选假设 H1:A, B两种键盘的打字出错率存在明显区别。
检验类型
检验类型有很多种,因为该使用两组数据是独立的样本,所以为双样本独立检验。
抽样分布类型
我们还要判断抽样分布是哪种?因为抽样分布的类型,决定了后面计算p值的不同。
在我们这个案例中,样本大小是25(小于30),属于小样本。那小样本的抽样分布是否满足t分布呢?因为t分布还要求数据集近似正态分布,所以下面图片我们看下差值数据集的分布长什么样。
#导入绘图包
import seaborn as sns
#查看数据集分布
sns.distplot(data['A'])
plt.title('A键盘出错字数分布')
plt.show()
sns.distplot(data['B'])
plt.title('B键盘出错字数分布')
plt.show()

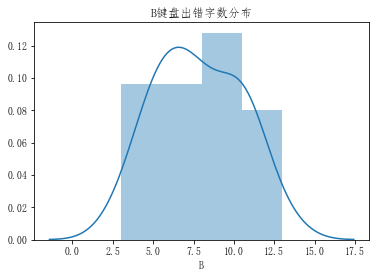
通过观察上面差值数据集分布图,数据集近似正态分布,所以满足t分布的使用条件,我们可以使用双样本独立t检验。
检验方向
单尾检验(左尾,右尾),还是双尾检验?
因为备选假设是:A,B两键盘打字出错数是否存在明显区别。
所以我们使用双独立样本t检验,双尾检验。显著水平为5%
2.证据是什么?
在零假设成立前提下,得到样本平均值的概率 p 是多少?
'''
用python统计包scipy自动计算
用scipy计算出的是:双尾检验
单(1samp)样本t检验(ttest_1samp):https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_1samp.html
相关(related)配对t检验(ttest_rel):https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_rel.html
双独立(independent)样本t检验(ttest_ind):https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html
'''
#导入统计模块(stats)
from scipy import stats
'''
ttest_ind:相关配对检验
返回值
第1个值t是假设检验计算出的(t值),
第2个值p是双尾检验的p值
'''
t,p_twoTail = stats.ttest_ind(data['A'],data['B'])
print('t值=',t,'双尾检验的p值=',p_twoTail)
t值= -4.055938536857321 双尾检验的p值= 0.0001825606172014822
上述分析结果可见,基于 scipy 的双样本独立t检验无法返回自由度 t,对于后期计算置信区间不变,因此建议使用 statsmodels 模块进行分析,如下:
'''
双独立(independent)样本t检验(ttest_ind)
statsmodels.stats.weightstats.ttest_ind
官网使用文档http://www.statsmodels.org/dev/generated/statsmodels.stats.weightstats.ttest_ind.html
'''
import statsmodels.stats.weightstats as st
'''
ttest_ind:独立双样本t检验,
usevar='unequal'两个总体方差不一样
返回值
第1个值t是假设检验计算出的(t值),
第2个p_two是双尾检验的p值
第3个df是独立双样本的自由度
'''
t,p_two,df=st.ttest_ind(data['A'],data['B'],
usevar='unequal')
#自由度一般只保留整数部分
print('t=',t,'p_two=',p_twoTail,',df=',df)
t= -4.055938536857321 p_two= 0.0001825606172014822 ,df= 45.27813331135627
3.判断标准是什么?
#显著水平使用alpha=5%
alpha=0.05
4.做出结论
本次分析的直接是双尾检验,因此p直接与alpha进行对比
#显著水平
a=0.05
#决策
if(p_twoTail< a):
print('拒绝零假设,有统计显著')
print('也就是接受备选假设:AB键盘打字出错数存在明显差异')
else:
print('接受备选假设,没有统计显著,也就是AB键盘不存在明显差异')
# 结果:
#拒绝零假设,有统计显著
#也就是接受备选假设:AB键盘打字出错数存在明显差异
假设检验报告:
双样本独立检验 t(45)=-4.06, p=0.00018 (α=5%),双尾检验
统计上存在显著差异,拒绝零假设,说明 A,B 键盘存在明显差异。
5.置信区间
1)置信水平对应的t值(t_ci)
查 t 表格可以得到,95%的置信水平对应的 t值=2.0141 (此处用的自由度是 statsmodels 计算出来的自由度 45,)
95%的置信水平,自由度是 n-1 对应的 t 值
查找t表格获取,也可以通过这个工具获取:graphpad
2)计算上下限
置信区间上限a=样本平均值 - t_ci ×标准误差
置信区间下限b=样本平均值 - t_ci ×标准误差
代入计算如下
t_ci=2.0141
#差值数据集平均值
sample_mean=A_mean-B_mean
#使用双样本独立假设的标准差计算公式
se=np.sqrt(np.square(A_std)/25+np.square(B_std)/25)
#置信区间上限
a=sample_mean - t_ci * se
#置信区间下限
b=sample_mean + t_ci * se
print('两个平均值差值的置信区间,95置信水平 CI=[%f,%f]' % (a,b))
两个平均值差值的置信区间,95置信水平 CI=[-4.070699,-1.369301]
可见,A键盘相对B键盘的出错数要小1-4个左右。
6.效应量
一般需要在报告中给出效应量(effect size)。
什么是效应量呢?
效应量是指处理效应的大小,例如药物A比药物B效果显著。度量效应量有很多种,但大多数都属于两大主要类别。
1)第一种叫做差异度量
例如在对比平均值时,衡量效应大小的常见标准之一是Cohen’s d
Cohen’s d = (样本平均值1-样本平均值2) / 标准差
Cohen’s d 除以的是标准差,也就是以标准差为单位,样本平均值和总体平均值之间相差多少。
Cohen’s d的评价标准为:
小效应(≥0.2且<0.5);中等效应(≥0.5且<0.8);大效应(≥0.8)。
2)第二种叫做相关度度量
例如R平方,表示某个变量的变化比例与另一变量的关系。可以用t检验的信息推出R平方的公式,这里的t值从t检验中获得的值,df 是自由度。
$ r^2 = t_2 / (t_2 + df)$
如果 $r^2$ 等于20%,表示我们可以说通过知道另一个变量能够接受相关变量20%的变化情况
相关度指标的评价标准为:
小效应(≥0.01且<0.09);中等效应(≥0.09且<0.25);大效应(≥0.25)。
'''
效应量:差异指标Cohen's d
'''
#差值数据集的合并标准差
sample_std=np.sqrt((24*np.square(A_std)+24*np.square(B_std))/48)
#计算效应量
d1=(A_mean - B_mean) / sample_std
print('d=',d1)
#d= -1.1471926574
d= -1.147192657395062
四、数据分析报告总结
1、描述统计分析
第一组数据:A键盘,实验者的打字平均出错数是: 5.08 个,标准差是 2.05993527406405 个
第二组数据:B键盘,实验者的打字平均出错数是: 7.8 个,标准差是 2.6457513110645903 个
可见,A键盘的打字出错数小于B键盘
2、推论统计分析
1)假设检验
双样本独立检验t(45)=-4.06,p=0.00018 (α=5%),双尾检验
统计上存在显著差异,拒绝零假设,从而验证AB键盘存在显著差异。
2)置信区间
两个平均值差值的置信区间,95%置信水平 CI=[-4.070699,-1.369301]
3)效应量
d= - 1.147