相关(Correlation)描述的是两个变量X和Y之间的联系紧密程度,而回归(Regression)则是度量X变量对Y变量的线性影响大小。
相关(Correlation)描述的是两个变量X和Y之间的联系紧密程度,而回归(Regression)则是度量X变量对Y变量的线性影响大小。常用表示相关性的系数为皮尔相关系数(Pearson correlation coefficient),简称相关系数(Correlation coefficient),其值介于 - 1与 1 之间。同时,我们在中学数学直线方程(y = a + bx )常常提到的斜率b,即是回归系数(Regression coefficient)的一种表现形式,其值介于 -∞ 与 +∞ 之间。
举一个生活中的例子来形象的说明相关和回归之间的差异。先假定群体中20-30岁成年男子的身高普遍分布于160至190cm之间,而体重普遍分布于45至100kg之间,那我们会对成年男子的身高和体重间的相关和回归情况有什么样的预判?当然,我们会推断身高越高的男子有更多体重的趋势。下面图1中1a、和1b分别是l两组具有同等身高组合,却有不同体重分布的散点图,由红色的直线表示预测其体重与身高的直线方程。两组男子身高和体重的回归系数都为1.1(即斜率为1.1),相关系数则分别为0.9和0.5。仔细观察发现,在相同回归系数的情况下,相关系数越高的组,实际体重越接近直线方程的预测值。从直线方程的预测性角度看,虽然回归系数一直,但相关系数越高的一组,预测准确度也越高。
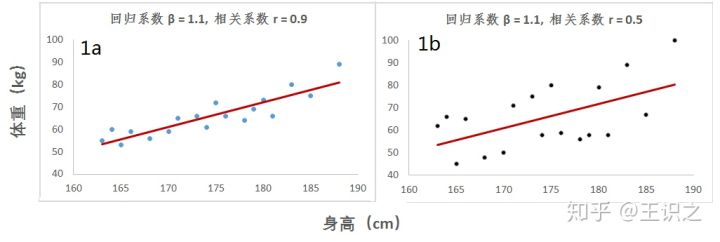
图一,相同的回归系数,不同的相关系数
再换一个角度去解读相关与回归的差异。假设,我们的推断是越高的男子,更趋向于有更小的体重呢(虽然有悖于事实)?请看图2,我们将图1a男子组的体重按照身高的高低颠倒排序,相关系数由图2a中的0.9变为了图2b中的-0.9,虽然两种情况下相关系数的绝对值一致。
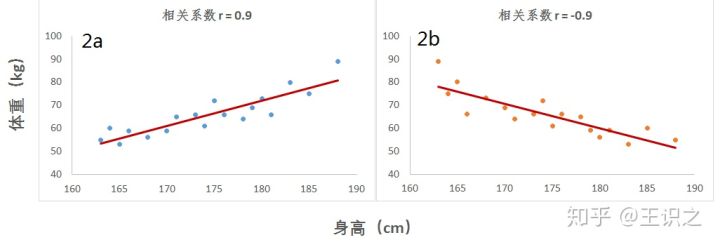
图二,相同相关系数绝对值,不同的趋势方向
相关和回归数值的大小存在着内在的联系,这是导致这两个统计概念难以辨析的原因。通常,相关系数绝对值越大的两组变量间,回归系数的绝对值也越高; 而当相关系数为0时,两组变量间的回归系数也是无法求解的。笔者所理解的其间微妙差异在于,相关是关系强度的定量,而回归是关系趋势的定向。