Welcome to my blog
这里是我建立的个人小天地哦 ! 🤣🤣🤣-
如何设置 Markdown 图片的大小、居中
在 markdown 中插入图片的时候,一般情况下是靠左侧的,在 markdown 也可以使用
HTML语法进行图片的插入,来方便控制图片的大小和位置。
-
最小二乘法
-
最大熵模型
最大熵模型(maximum entropy model, MaxEnt)也是很典型的分类算法了,它和逻辑回归类似,都是属于对数线性分类模型。在损失函数优化的过程中,使用了和支持向量机类似的凸优化技术。理解了最大熵模型,对逻辑回归,支持向量机以及决策树算法都会加深理解。
-
损失函数 正则化 范数
损失函数
损失函数和代价函数是同一个东西,目标函数是一个与他们相关但更广的概念,对于目标函数来说在有约束条件下的最小化就是损失函数(loss function)。
举个例子解释一下:(图片来自Andrew Ng Machine Learning公开课视频)
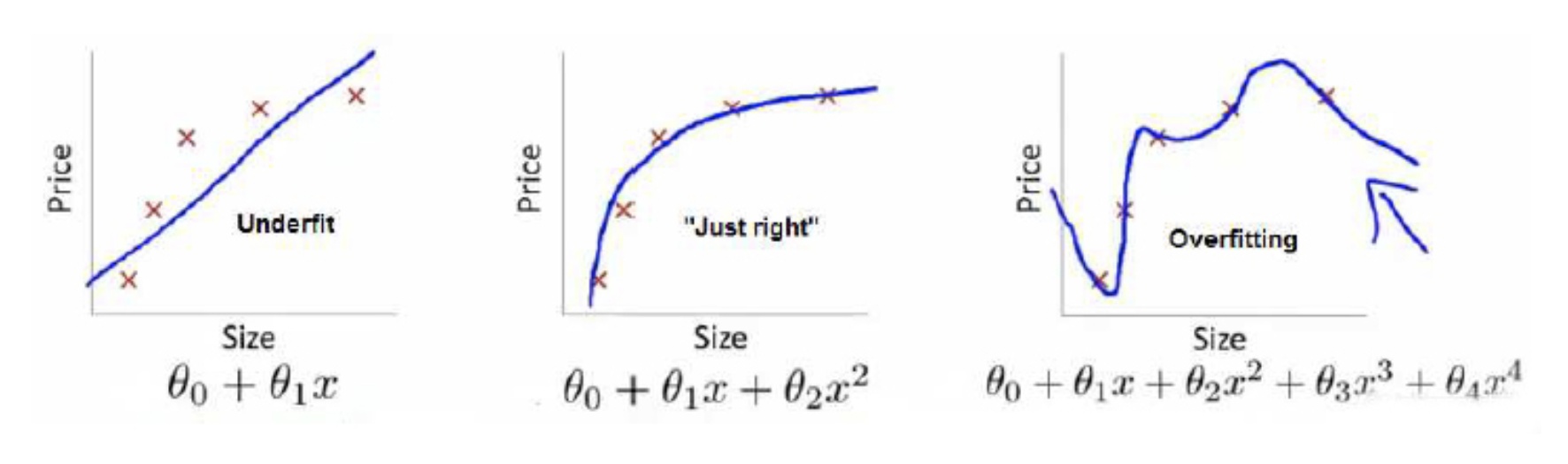
上面三个图的函数依次为 \(f_{1}(x), f_{2}(x), f_{3}(x)\) 。我们是想用这三个函数分别来拟合Price,Price的真实值记为 $Y$ 。
我们给定 $x$ ,这三个函数都会输出一个 $f(x)$ , 这个输出的 $f(x)$ 与真实值 $Y$ 可能是相同的,也可能是不同的,为了表示我们拟合的好坏,我们就用一个函数来度量拟合的程度,比如:
\[\begin{equation}L(Y, f(X))=\frac{1}{2} \sum_{i=1}^{N}(Y-f(X))^{2}\end{equation}\]个函数就称为损失函数(loss function),或者叫代价函数(cost function)。损失函数越小,就代表模型拟合的越好。损失函数为平方损失。系数 $\frac{1}{2}$ 为了计算方便
-
网络整理的 icon 、image 网站
刚把自己的小博客建立好 !就想搞点东西进去!由于最近发现自己浏览器里面的收藏的东西有点多,趁这个机会就整理一下! 这一片主要是关于图片、图标的 !大部分都是网上整理的 。
-
精确率与召回率,RoC曲线与PR曲线
在机器学习的算法评估中,尤其是分类算法评估中,我们经常听到精确率(precision)与召回率(recall),RoC曲线与PR曲线这些概念,那这些概念到底有什么用处呢?
-
最小二乘法
最小二乘法是用来做函数拟合或者求函数极值的方法。在机器学习,尤其是回归模型中,经常可以看到最小二乘法的身影 。
-
成功搭建自己的博客 !

总算是搞好啦 !! 😄
-
Markdown中内嵌HTML表格
自己在
Markdown中使用内置的表格时候,不太好控制。在网上搜索了一下,Markdown也可以使用HTML格式的表格,两者相比之下,选择使用HTML格式的表格 !下面是表格的基本内容,并不完全 !