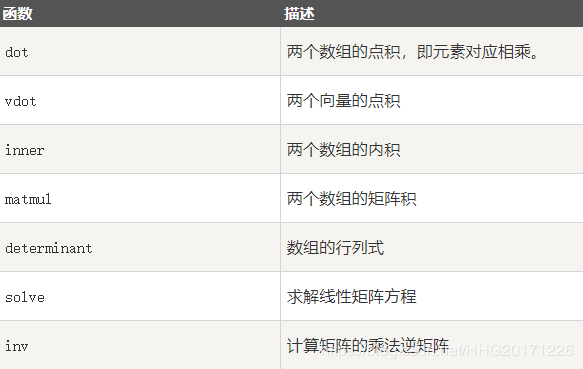
NumPy 线性代数中的运算
NumPy 提供了线性代数函数库 linalg,该库包含了线性代 数所需的所有功能 。
矩阵和向量积
numpy.dot()
numpy.dot()对于两个一维的数组,计算的是这两个数组对应下标元素的乘积和(数学上称之为内积);对于二维数组,计算的是两个数组的矩阵乘积;对于多维数组,它的通用计算公式如下,即结果数组中的每个元素都是:数组a的最后一维上的所有元素与数组b的倒数第二位上的所有元素的乘积和:
numpy.dot(a, b, out=None)
参数说明:
- a : ndarray 数组
- b : ndarray 数组
- out : ndarray, 可选,用来保存dot()的计算结果
import numpy.matlib
import numpy as np
a = np.array([[1,2],[3,4]])
b = np.array([[11,12],[13,14]])
print(np.dot(a,b))
[[37 40]
[85 92]]
[[1*11+2*13, 1*12+2*14],[3*11+4*13, 3*12+4*14]]
numpy.vdot()
numpy.vdot() 函数是两个向量的点积。 如果第一个参数是复数,那么它的共轭复数会用于计算。 如果参数是多维数组,它会被展开。
请注意,vdot处理多维数组的方式与dot不同:不是执行矩阵乘积,而是先将输入参数平铺到1-D向量。因此,它应该只用于向量。
>>> a = np.array([1+2j,3+4j])
>>> b = np.array([5+6j,7+8j])
>>> np.vdot(a, b)
(70-8j)
>>> np.vdot(b, a)
(70+8j)
numpy.inner()
两个数组的内积。
用于1-D数组(没有复共轭)的向量的普通内积,在较高维度上是最后轴上的和积。
import numpy as np
print (np.inner(np.array([1,2,3]),np.array([0,1,0])))
# 等价于 1*0+2*1+3*0
多维数组实例
import numpy as np
a = np.array([[1,2], [3,4]])
print ('数组 a:')
print (a)
数组 a:
[[1 2]
[3 4]]
b = np.array([[11, 12], [13, 14]])
print ('数组 b:')
print (b)
数组 b:
[[11 12]
[13 14]]
print ('内积:')
print (np.inner(a,b))
内积:
[[35 41]
[81 95]]
内积计算式为:
1*11+2*12, 1*13+2*14
3*11+4*12, 3*13+4*14
矩阵特征值
numpy.linalg.eig
numpy.linalg.eig(a) 计算正方形数组的特征值和右特征向量。
参数:
- a:(...,M,M)数组 将计算特征值和右特征向量的矩阵
返回:
- w:(...,M)数组
特征值,每个根据其多重性重复。特征值不必是有序的。结果数组将是复杂类型,除非虚部为零,在这种情况下,它将被转换为实数类型。当a是实数时,得到的特征值将是实数(0虚数部分)或出现在共轭对
- v:(...,M,M)数组
归一化(单位“长度”)特征向量,使得列
v[:,i]是对应于特征值w[i]
当我们想要求解一个非方阵的奇异值之前,我们需要先把这个矩阵转换为方阵。
>>> from numpy import *
>>> import numpy as np
>>> A = mat([[4,5,6],[1,2,3]])
>>> U = A*A.T
>>> lamda,hU=linalg.eig(U)
>>> sigma=sqrt(lamda)
>>> print sigma
[9.508032 0.77286964]
在开头先进行矩阵的乘法,把矩阵和矩阵的转置相乘,得到一个方阵,然后这个方阵作为参数,可以得到特征值和特征向量。
其中返回的第一个值w进行开根号就是data这个矩阵的奇异值。
可以用svd函数来验证一下。
>>> Q,S,VT=linalg.svd(A)
>>> print S
[9.508032 0.77286964]
参考:
numpy.linalg.solve()
numpy.linalg.solve(a,b)函数给出了矩阵形式的线性方程的解。
计算良好确定的,即满秩线性矩阵方程ax = b的“精确”解,x。
a:(...,M,M)array_like
系数矩阵。
b:{(...,M,),(...,M,K)},array_like
纵坐标或“因变量”值。
返回:
x:{(...,M,),(...,M,K)} ndarray
a x = b。返回形状与b相同。
求解方程 3 * x0 + x1 = 9和 x0 + 2 x1 = 8
>>> a = np.array([[3,1], [1,2]])
>>> b = np.array([9,8])
>>> x = np.linalg.solve(a, b)
>>> x
array([ 2., 3.])
numpy.linalg.inv()
numpy.linalg.inv(a) 函数计算矩阵的乘法逆矩阵。
逆矩阵(inverse matrix):设A是数域上的一个n阶矩阵,若在相同数域上存在另一个n阶矩阵B,使得: AB=BA=E ,则我们称B是A的逆矩阵,而A则被称为可逆矩阵。注:E为单位矩阵。
import numpy as np
a = np.array([[1,1,1],[0,2,5],[2,5,-1]])
print ('数组 a:')
print (a)
数组 a:
[[ 1 1 1]
[ 0 2 5]
[ 2 5 -1]]
ainv = np.linalg.inv(a)
print ('a 的逆:')
print (ainv)
a 的逆:
[[ 1.28571429 -0.28571429 -0.14285714]
[-0.47619048 0.14285714 0.23809524]
[ 0.19047619 0.14285714 -0.0952381 ]]
print ('矩阵 b:')
b = np.array([[6],[-4],[27]])
print (b)
矩阵 b:
[[ 6]
[-4]
[27]]
print ('计算:A^(-1)B:')
x = np.linalg.solve(a,b)
print (x)
计算:A^(-1)B:
[[ 5.]
[ 3.]
[-2.]]
# 这就是线性方向 x = 5, y = 3, z = -2 的解
矩阵分解
numpy.linalg.svd函数
奇异值分解
函数:np.linalg.svd(a,full_matrices=1,compute_uv=1)
参数:
a是一个形如(M,N)矩阵full_matrices的取值是为0或者1,默认值为1,这时u的大小为(M,M),v的大小为(N,N) 。否则u的大小为(M,K),v的大小为(K,N) ,K=min(M,N)。compute_uv的取值是为0或者1,默认值为1,表示计算u,s,v。为0的时候只计算s。
返回
- 总共有三个返回值u,s,v
- u大小为(M,M),s大小为(M,N),v大小为(N,N)。
- A = usv
- 其中s是对矩阵a的奇异值分解。s除了对角元素不为0,其他元素都为0,并且对角元素从大到小排列。s中有n个奇异值,一般排在后面的比较接近0,所以仅保留比较大的r个奇异值。
>>> from numpy import *
>>> data = mat([[1,2,3],[4,5,6]])
>>> U,sigma,VT = np.linalg.svd(data)
>>> print U
[[-0.3863177 -0.92236578]
[-0.92236578 0.3863177 ]]
>>> print sigma
[9.508032 0.77286964]
>>> print VT
[[-0.42866713 -0.56630692 -0.7039467 ]
[ 0.80596391 0.11238241 -0.58119908]
[ 0.40824829 -0.81649658 0.40824829]]
有几点需要注意的地方:
- python 中的 svd 分解得到的 VT 就是 V 的转置,这一点与matlab中不一样,matlab中svd后得到的是V,如果要还原的话还需要将V转置一次,而Python中不需要。
- Python 中 svd 后得到的sigma是一个行向量,Python中为了节省空间只保留了A的奇异值,所以我们需要将它还原为奇异值矩阵。同时需要注意的是,比如一个5
*5大小的矩阵的奇异值只有两个,但是他的奇异值矩阵应该是5*5的,所以后面的我们需要手动补零,并不能直接使用diag将sigma对角化。
关于奇异值的解释:
numpy.linalg.det()
numpy.linalg.det() 函数计算输入矩阵的行列式。
行列式在线性代数中是非常有用的值。 它从方阵的对角元素计算。 对于 2×2 矩阵,它是左上和右下元素的乘积与其他两个的乘积的差。
换句话说,对于矩阵[[a,b],[c,d]],行列式计算为 ad-bc。 较大的方阵被认为是 2×2 矩阵的组合。
import numpy as np
a = np.array([[1,2], [3,4]])
print (np.linalg.det(a))
-2.0
import numpy as np
b = np.array([[6,1,1], [4, -2, 5], [2,8,7]])
print (b)
print (np.linalg.det(b))
print (6*(-2*7 - 5*8) - 1*(4*7 - 5*2) + 1*(4*8 - -2*2))
[[ 6 1 1]
[ 4 -2 5]
[ 2 8 7]]
-306.0
-306