求解特征值和特征向量
scipy.linalg.eig(a,
b=None,
left=False,
right=True,
overwrite_a=False,
overwrite_b=False,
check_finite=True)
a:一个方阵,形状为(M,M)。待求解特征值和特征向量的矩阵。b:默认为None,表示求解标准的特征值问题: Ax=λx。 也可以是一个形状与a相同的方阵,此时表示广义特征值问题: Ax=λBxleft:一个布尔值。如果为True,则计算左特征向量right:一个布尔值。如果为True,则计算右特征向量overwrite_a:一个布尔值,指定是否将结果写到a的存储区。overwrite_b:一个布尔值,指定是否将结果写到b的存储区。check_finite:如果为True,则检测输入中是否有nan或者inf
返回值:
w:一个一维数组,代表了M特特征值。vl:一个数组,形状为(M,M),表示正则化的左特征向量(每个特征向量占据一列,而不是一行)。仅当left=True时返回vr:一个数组,形状为(M,M),表示正则化的右特征向量(每个特征向量占据一列,而不是一行)。仅当right=True时返回
numpy提供了numpy.linalg.eig(a)来计算特征值和特征向量
有特征值:Axr=λxr ; 左特征值: 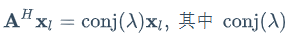 为特征值的共轭。
为特征值的共轭。
令 P=[xr1,xr2,⋯,xrM]
Σ=⎣⎢⎢⎡λ10⋮00λ2⋮000⋮0⋯⋯⋱⋯00⋮λM⎦⎥⎥⎤
则有:
AP=PΣ⟹A=PΣP−1
求解问题
linalg.eig(A)
linalg.eigvals(A)
linalg.eig(A, B)
- 求解 Av=λBv 的问题
基本使用
例子
矩阵为:
A=⎣⎡123546212⎦⎤
特征多项式为:
∣A−λI∣==(1−λ)[(4−λ)(2−λ)−6]−5[2(2−λ)−3]+2[12−3(4−λ)]−λ3+7λ2+8λ−3
特征根为:
λ1=7.9579λ2=−1.2577λ3=0.2997
求解特征值和特征向量
⎣⎡123546212⎦⎤
import numpy as np
from scipy.linalg import eig
a = np.array([[1,5,2],[2,4,1],[3,6,2]])
w,vr=eig(a,right=True)
print(w)
print(vr)
结果:
# 每一个为一个特征值
[ 7.9579162 +0.j -1.25766471+0.j 0.2997485 +0.j]
# 每一列对应一个特征值的特征向量
[[-0.5297175 -0.90730751 0.28380519]
[-0.44941741 0.28662547 -0.39012063]
[-0.71932146 0.30763439 0.87593408]]