Jacobian矩阵和Hessian矩阵
在向量分析中, 雅可比矩阵是一阶偏导数以一定方式排列成的矩阵, 其行列式称为雅可比行列式. 还有, 在代数几何中, 代数曲线的雅可比量表示雅可比簇:伴随该曲线的一个代数群, 曲线可以嵌入其中. 它们全部都以数学家卡尔·雅可比(Carl Jacob, 1804年10月4日-1851年2月18日)命名;
一、雅可比矩阵
雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近. 因此, 雅可比矩阵类似于多元函数的导数.
假设 Rn→Rm 是一个从欧式n维空间转换到欧式m维空间的函数.
⎩⎪⎪⎨⎪⎪⎧y1=f1(x1,…,xn)y2=f2(x1,…,xn)⋯ym=fn(x1,…,xn)
这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵, 这就是所谓的雅可比矩阵:
J=[∂x1∂f⋯∂xn∂f]=⎣⎢⎢⎢⎡∂x1∂f1⋮∂x1∂fm⋯⋱⋯∂xn∂f1⋮∂xn∂fm⎦⎥⎥⎥⎤
此矩阵表示为:JF(x1,…,xn)
如果 p 是 Rn 中的一点, F 在 p点可微分, 那么在这一点的导数由 JF(p) 给出(这是求该点导数最简便的方法). 在此情况下, 由 F(p) 描述的线性算子即接近点 p 的 F 的最优线性逼近, 逼近于:

与泰勒一阶展开近似
二、雅可比行列式
如果m = n, 那么 F 是从 n 维空间到 n 维空间的函数, 且它的雅可比矩阵是一个方块矩阵. 于是我们可以取它的行列式, 称为雅可比行列式.
在某个给定点的雅可比行列式提供了 在接近该点时的表现的重要信息.
- 如果连续可微函数 F 在 p 点的雅可比行列式不是零, 那么它在该点附近具有反函数. 这称为反函数定理. 更进一步,
- 如果 p 点的雅可比行列式是正数, 则 F 在 p 点的取向不变;
- 如果是负数, 则 F 的取向相反
而从雅可比行列式的绝对值, 就可以知道函数 F 在 p 点的缩放因子;这就是为什么它出现在换元积分法中.
对于取向问题可以这么理解, 例如一个物体在平面上匀速运动, 如果施加一个正方向的力 F , 即取向相同, 则加速运动, 类比于速度的导数加速度为正;如果施加一个反方向的力 F , 即取向相反, 则减速运动, 类比于速度的导数加速度为负.
三、海森Hessian矩阵
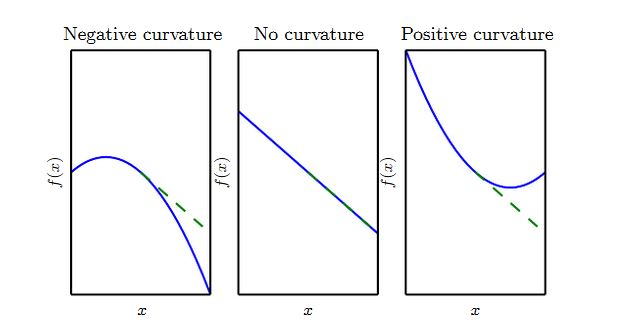
二阶导数 f′′(x) 刻画了曲率。假设有一个二次函数(实际任务中,很多函数不是二次的,但是在局部可以近似为二次函数):
如果函数的二阶导数为零,则它是一条直线。如果梯度为 1,则当沿着负梯度的步长为 ϵ 时,函数值减少ϵ 。
如果函数的二阶导数为负,则函数向下弯曲。如果梯度为1,则当沿着负梯度的步长为 ϵ 时,函数值减少的量大于 ϵ 。
如果函数的二阶导数为正,则函数向上弯曲。如果梯度为1,则当沿着负梯度的步长为 ϵ 时,函数值减少的量少于 ϵ 。
在数学中, 海森矩阵(Hessian matrix或Hessian)是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵, 此函数如下:
f(x1,x2…,xn)
如果 f 的所有二阶导数都存在, 那么 f 的海森矩阵即:
H(f)ij(x)=DiDjf(x)
其中 x=(x1,x2…,xn) 即 H(f) 为:
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡∂x12∂2f∂x2∂x1∂2f⋮∂xn∂x1∂2f∂x1∂x2∂2f∂x22∂2f⋮∂xn∂x2∂2f⋯⋯⋱⋯∂x1∂xn∂2f∂x2∂xn∂2f⋮∂xn2∂2f⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
即海森矩阵的第 i 行 j 列元素为:Hi,j=∂xi∂xj∂2f(x⃗)
海森矩阵被应用于牛顿法解决的大规模优化问题.
当二阶偏导是连续时,海森矩阵是对称阵,即有: H=HT
对于特定方向 d⃗ 上的二阶导数为:d⃗THd⃗ 。
- 如果 d⃗ 是海森矩阵的特征向量,则该方向的二阶导数就是对应的特征值。
- 如果 d⃗ 不是海森矩阵的特征向量,则该方向的二阶导数就是所有特征值的加权平均,权重在
(0,1)之间。且与 d⃗ 夹角越小的特征向量对应的特征值具有更大的权重。
- 最大特征值确定了最大二阶导数,最小特征值确定最小二阶导数。
四、海森矩阵与学习率
将 f(x⃗) 在 x0⃗ 处泰勒展开:f(x⃗)≈f(x⃗0)+(x⃗−x⃗0)Tg⃗+21(x⃗−x⃗0)TH(x⃗−x⃗0) 。其中: g⃗ 为 x0⃗ 处的梯度 ;H 为 x0⃗ 处的海森矩阵。
根据梯度下降法:x⃗′=x⃗−ϵ∇x⃗f(x⃗)
应用在点 x0⃗ ,有:f(x⃗0−ϵg⃗)≈f(x⃗0)−ϵg⃗Tg⃗+21ϵ2g⃗THg⃗
- 第一项代表函数在点 x0⃗ 处的值。
- 第二项代表由于斜率的存在,导致函数值的变化。
- 第三项代表由于曲率的存在,对于函数值变化的矫正。
注意:如果 21ϵ2g⃗THg⃗ 较大,则很有可能导致:沿着负梯度的方向,函数值反而增加!
如果 g⃗THg⃗≤0,则无论 ϵ 取多大的值, 可以保证函数值是减小的。
如果 g⃗THg⃗>0 ,则学习率 ϵ 不能太大。若 ϵ 太大则函数值增加。
根据 f(x⃗0−ϵg⃗)−f(x⃗0)<0 ,则需要满足:ϵ<g⃗THg⃗2g⃗Tg⃗ 。若 ϵ≥g⃗THg⃗2g⃗Tg⃗ ,则会导致沿着负梯度的方向函数值在增加。
考虑最速下降法,选择使得 f 下降最快的 ϵ ,则有:ϵ∗=argminϵ,ϵ>0f(x⃗0−ϵg⃗) 。求解 ∂ϵ∂f(x⃗0−ϵg⃗)=0 有 :ϵ∗=g⃗THg⃗g⃗Tg⃗ 。
根据 g⃗THg⃗>0 ,很明显有: :ϵ<g⃗THg⃗2g⃗Tg⃗ 。
由于海森矩阵为实对称阵,因此它可以进行特征值分解。假设其特征值从大到小排列为:λ1≥λ2≥⋯≥λn 。
海森矩阵的瑞利商为:R(x⃗)=x⃗Tx⃗x⃗THx⃗,x⃗≠0⃗ 。可以证明:
λnλ1λn≤R(x⃗)≤λ1=x⃗≠0⃗maxR(x⃗)=x⃗≠0⃗minR(x⃗)
根据 ϵ∗=g⃗THg⃗g⃗Tg⃗=R(g⃗)1 可知:海森矩阵决定了学习率的取值范围。最坏的情况下,梯度 g⃗与海森矩阵最大特征值 λ1 对应的特征向量平行,则此时最优学习率为 λ11 。
五、驻点与全局极小点
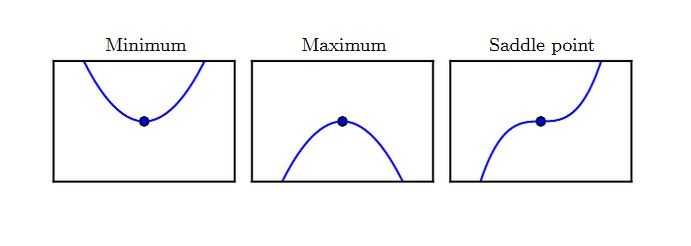
满足导数为零的点(即 f′′(x)=0)称作驻点。驻点可能为下面三种类型之一:
- 局部极小点:在 x 的一个邻域内,该点的值最小。
- 局部极大点:在 x 的一个邻域内,该点的值最大。
- 鞍点:既不是局部极小,也不是局部极大。
全局极小点: x∗=argminxf(x)
二阶导数可以配合一阶导数来决定驻点的类型:
- 局部极小点: f′(x)=0,f′′(x)>0 。
- 局部极大点: f′(x)=0,f′′(x)<0。
- f′(x)=0,f′′(x)=0 :驻点的类型可能为任意三者之一。
对于多维的情况类似有:
局部极小点:∇xf(x)=0 ,且海森矩阵为正定的(即所有的特征值都是正的),当海森矩阵为正定时,任意方向的二阶偏导数都是正的。
局部极大点:∇xf(x)=0,且海森矩阵为负定的(即所有的特征值都是负的)。
当海森矩阵为负定时,任意方向的二阶偏导数都是负的。
∇xf(x)=0 ,且海森矩阵的特征值中至少一个正值、至少一个负值时,为鞍点。
当海森矩阵非上述情况时,驻点类型无法判断。
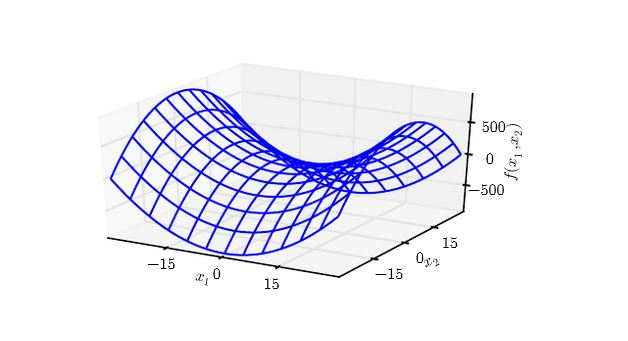
下图为 f(x)=x12−x22 在原点附近的等值线。其海森矩阵为一正一负。
- 沿着 x1 方向,曲线向上弯曲;沿着 x2 方向,曲线向下弯曲。
- 鞍点就是在一个横截面内的局部极小值,另一个横截面内的局部极大值。
参考




