梯度与梯度下降
一、导数
一张图读懂导数与微分:
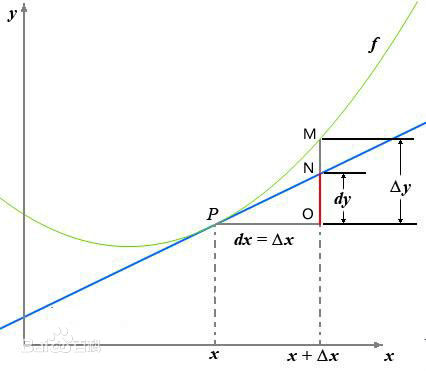
如果忘记了导数微分的概念,基本看着这张图就能全部想起来。 导数定义如下: 反映的是函数 在某一点处沿 轴正方向的变化率。再强调一遍,是函数 在 轴上某一点处沿着 轴正方向的变化率/变化趋势。直观地看,也就是在 轴上某一点处,如果 ,说明 的函数值在 点沿 轴正方向是趋于增加的;如果 ,说明 的函数值在 x 点沿 x 轴正方向是趋于减少的。
这里补充上图中的 等符号的意义及关系如下:
- 的变化量;
- 的变化量 趋于0 时,则记作微元 ;
- ,是函数的增量;
,是切线的增量;
当 时, 与 都是无穷小, 是 的主部,即 .
二、导数和偏导数
偏导数的定义如下:
可以看到,导数与偏导数本质是一致的,都是当自变量的变化量趋于0时,函数值的变化量与自变量变化量比值的极限。直观地说,偏导数也就是函数在某一点上沿坐标轴正方向的的变化率。
区别在于:
- 导数,指的是一元函数中,函数 在某一点处沿x轴正方向的变化率;
- 偏导数,指的是多元函数中,函数 在某一点处沿某一坐标轴正方向的变化率。
三、导数与方向导数
方向导数的定义如下:
在前面导数和偏导数的定义中,均是沿坐标轴正方向讨论函数的变化率。那么当我们讨论函数沿任意方向的变化率时,也就引出了方向导数的定义,即:某一点在某一趋近方向上的导数值。
通俗的解释是:
我们不仅要知道函数在坐标轴正方向上的变化率(即偏导数),而且还要设法求得函数在其他特定方向上的变化率。而方向导数就是函数在其他特定方向上的变化率。
四、导数与梯度
标量函数 的梯度表示为: 或 ,其中 (nabla)表示向量微分算子。
梯度定义如下:
函数在某一点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。
一般的多元函数的梯度:
且其偏导数存在,则 的梯度 为一向量函数。
4.1 对向量的梯度
以 n×1实向量x为变元的实标量函数 相对于x的梯度为一n×1列向量x,定义为: m 维行向量函数 相对于 n 维实向量x的梯度为一n×m矩阵,定义为
4.2 对矩阵的梯度
实标量函数 相对于m×n实矩阵A的梯度为一m×n矩阵,简称梯度矩阵,定义为
梯度的提出只为回答一个问题:
函数在变量空间的某一点处,沿着哪一个方向有最大的变化率?
这里注意三点:
1)梯度是一个向量,即有方向有大小;
2)梯度的方向是最大方向导数的方向;
3)梯度的值是最大方向导数的值。
五、导数与向量
提问:导数与偏导数与方向导数是向量么?
向量的定义是有方向(direction)有大小(magnitude)的量。
从前面的定义可以这样看出,偏导数和方向导数表达的是函数在某一点沿某一方向的变化率,也是具有方向和大小的。因此从这个角度来理解,我们也可以把偏导数和方向导数看作是一个向量,向量的方向就是变化率的方向,向量的模,就是变化率的大小。
那么沿着这样一种思路,就可以如下理解梯度:
梯度即函数在某一点最大的方向导数,函数沿梯度方向函数有最大的变化率。
六、梯度下降法
6.1 梯度下降的直观解释
首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置,由于我们不知道怎么下山,于是决定走一步算一步,也就是在每走到一个位置的时候,求解当前位置的梯度,沿着梯度的负方向,也就是当前最陡峭的位置向下走一步,然后继续求解当前位置梯度,向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去,一直走到觉得我们已经到了山脚。当然这样走下去,有可能我们不能走到山脚,而是到了某一个局部的山峰低处。
从上面的解释可以看出,梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。

6.2 梯度下降的相关概念
在详细了解梯度下降的算法之前,我们先看看相关的一些概念。
步长(Learning rate)
步长决定了在梯度下降迭代的过程中,每一步沿梯度负方向前进的长度。用上面下山的例子,步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。
特征(feature)
指的是样本中输入部分,比如2个单特征的样本 ,则第一个样本特征为 , 第一个样本输出为 。
假设函数(hypothesis function)
在监督学习中,为了拟合输入样本,而使用的假设函数,记为 。比如对于单个特征的m个样本 , 可以采用拟合函数如下: .
损失函数(loss function)
为了评估模型拟合的好坏,通常用损失函数来度量拟合的程度。损失函数极小化,意味着拟合程度最好,对应的模型参数即为最优参数。在线性回归中,损失函数通常为样本输出和假设函数的差取平方。比如对于 m 个样本 , 采用线性回归,损失函数为:
其中 表示第 个样本特征, 表示第 个样本对应的输出, 为假设 函数。
6.3 梯度下降的详细算法
梯度下降法的算法可以有代数法和矩阵法(也称向量法)两种表示,如果对矩阵分析不熟悉,则代数法更加容易理解。不过矩阵法更加的简洁,且由于使用了矩阵,实现逻辑更加的一目了然。这里先介绍代数法,后介绍矩阵法。
梯度下降法的代数方式描述
1.先决条件: 确认优化模型的假设函数和损失函数。
比如对于线性回归,假设函数表示为 , 其中 为模型参数, 为每个样本的n个特征值。这个表示可以简化,我们增加一个特征 ,这样 。
同样是线性回归,对应于上面的假设函数,损失函数为:
2.算法相关参数初始化
主要是初始化 ,算法终止距离 以及步长 。在没有任何先验知识的时候,我喜欢将所有的 初始化为0, 将步长初始化为 1。在调优的时候再优化。
3.算法过程
1)确定当前位置的损失函数的梯度,对于 ,其梯度表达式如下:
2)用步长乘以损失函数的梯度,得到当前位置下降的距离,即 对应于前面登山例子中的某一步。
3)确定是否所有的 , 梯度下降的距离都小于 , 如果小于 则算法终止,当前所有的 即为最终结果。否则进入步骤4.
4)更新所有的 ,对于 ,其更新表达式如下。更新完毕后继续转入步骤1.
下面用线性回归的例子来具体描述梯度下降。假设我们的样本是 :
,
损失函数如前面先决条件所述:
则在算法过程步骤 1 中对于 的偏导数计算如下:
由于样本中没有 上式中令所有的 为1.
步骤4中 的更新表达式如下:
从这个例子可以看出当前点的梯度方向是由所有的样本决定的,加 是为了好理解。由于步长也为常数,他们的乘机也为常数,所以这里 可以用一个常数表示。
梯度下降法的矩阵方式描述
这一部分主要讲解梯度下降法的矩阵方式表述,相对于3.3.1的代数法,要求有一定的矩阵分析的基础知识,尤其是矩阵求导的知识。
1.先决条件:
和3.3.1类似, 需要确认优化模型的假设函数和损失函数。对于线性回归,假设函数
的矩阵表达方式为: , 其中, 假设函数 为 的向量 , 为 的向量 , 里面有n+1个代数法的模型参数。 为 维的矩阵。m 代表样本的个数,n+1代表样本的特征数。
2.算法相关参数初始化
向量可以初始化为默认值,或者调优后的值。算法终止距离 ,步长 和3.3.1比没有变化。
3.算法过程:
1)确定当前位置的损失函数的梯度,对于 向量,其梯度表达式如下:
2)用步长乘以损失函数的梯度,得到当前位置下降的距离,即 对应于前面登山例子中的某一步。
3)确定 向量里面的每个值,梯度下降的距离都小于 ,如果小于 则算法终止,当前 向量即为最终结果。否则进入步骤4.
4)更新 向量,其更新表达式如下。更新完毕后继续转入步骤1.
线性回归的例子来描述具体的算法过程。
损失函数对于 向量的偏导数计算如下:
步骤4中 向量的更新表达式如下:
对于3.3.1的代数法,可以看到矩阵法要简洁很多。这里面用到了矩阵求导链式法则,和两个矩阵求导的公式。
这里面用到了矩阵求导链式法则,和两个个矩阵求导的公式。
公式1: 为向量
公式2:为标量
6.4 梯度下降的算法调优
在使用梯度下降时,需要进行调优。哪些地方需要调优呢?
算法的步长选择 : 在前面的算法描述中,我提到取步长为1,但是实际上取值取决于数据样本,可以多取一些值,从大到小,分别运行算法,看看迭代效果,如果损失函数在变小,说明取值有效,否则要增大步长。前面说了。步长太大,会导致迭代过快,甚至有可能错过最优解。步长太小,迭代速度太慢,很长时间算法都不能结束。所以算法的步长需要多次运行后才能得到一个较为优的值。
算法参数的初始值选择。 初始值不同,获得的最小值也有可能不同,因此梯度下降求得的只是局部最小值;当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险,需要多次用不同初始值运行算法,关键损失函数的最小值,选择损失函数最小化的初值。
归一化。由于样本不同特征的取值范围不一样,可能导致迭代很慢,为了减少特征取值的影响,可以对特征数据归一化,也就是对于每个特征 x,求出它的期望 和标准差 std(x),然后转化为:
这样特征的新期望为0,新方差为1,迭代速度可以大大加快。
6.5 梯度下降法求极值
求下列函数的极小值:
# From calculation, it is expected that the local minimum occurs at x=9/4
cur_x = 6 # The algorithm starts at x=6
gamma = 0.01 # step size multiplier
precision = 0.00001
previous_step_size = cur_x
def df(x):
return 4 * x**3 - 9 * x**2
while previous_step_size > precision:
prev_x = cur_x
cur_x += -gamma * df(prev_x)
previous_step_size = abs(cur_x - prev_x)
print("The local minimum occurs at %f" % cur_x)
# The local minimum occurs at 2.249965
七、梯度下降法与最小二乘法
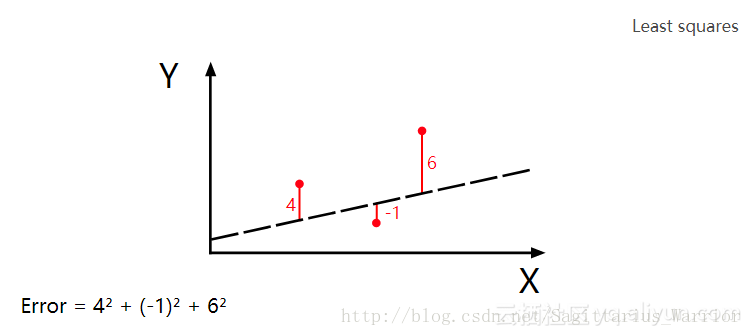
“机器学习”中有六个经典算法,其中就包括“最小二乘法”和“梯度下降法”,前者用于“搜索最小误差”,后者用于“用最快的速度搜索”,二者常常配合使用。代码演示如下:
# y = mx + b
# m is slope, b is y-intercept
def compute_error_for_line_given_points(b, m, coordinates):
totalerror = 0
for i in range(0, len(coordinates)):
x = coordinates[i][0]
y = coordinates[i][1]
totalerror += (y - (m * x + b)) ** 2
return totalerror / float(len(coordinates))
# example
compute_error_for_line_given_points(1, 2, [[3, 6], [6, 9], [12, 18]])
# 22.0
以上就是用“最小二乘法”来计算误差,当输入为 (1,2)(1,2) 时,输出为 22.0
很显然,最小二乘法需要不停地调整(试验)输入来找到一个最小误差。而应用“梯度下降法”,可以加快这个“试验”的过程。 以上面这段程序为例,误差是斜率 m 和常数 b 的二元函数,可以表示为 那么,对最小二乘法的参数调优就转变为了求这个二元函数的极值问题,也就是说可以应用“梯度下降法”了。
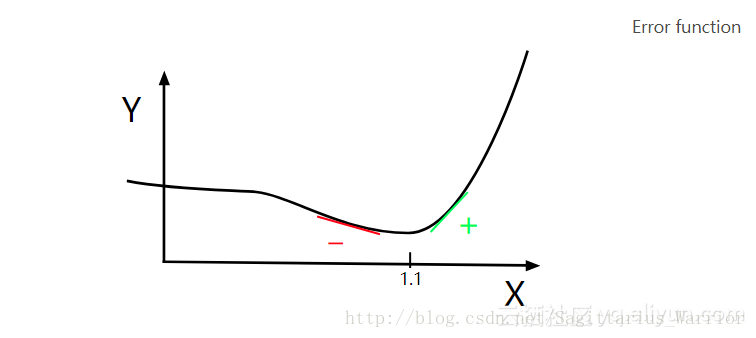
“梯度下降法”可以用于搜索函数的局部极值,如下,求下列函数的局部极小值 分析:这是一个一元连续函数,且可导,其导函数是:
根据“一阶导数极值判别法”:若函数 可导,且 在 的两侧异号,则 是 的极值点。那么,怎么找到这个 呢? 很简单,只需要沿斜率(导数值)的反方向逐步移动即可,如下图:导数为负时,沿x轴正向移动;导数为正时,沿x轴负方向移动。
current_x = 0.5 # the algorithm starts at x=0.5
learning_rate = 0.01 # step size multiplier
num_iterations = 60 # the number of times to train the function
# the derivative of the error function (x ** 4 = the power of 4 or x^4)
def slope_at_given_x_value(x):
return 5 * x ** 4 - 6 * x ** 2
# Move X to the right or left depending on the slope of the error function
x = [current_x]
for i in range(num_iterations):
previous_x = current_x
current_x += -learning_rate * slope_at_given_x_value(previous_x)
x.append(current_x) #print(previous_x)
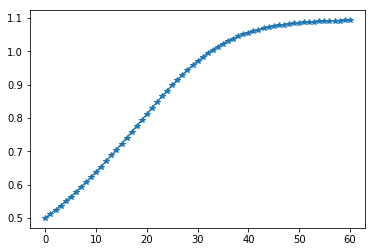
print("The local minimum occurs at %f, it is %f" % (current_x, current_x ** 5 - 2 * current_x ** 3 - 2))
The local minimum occurs at 1.092837, it is -3.051583
import numpy as np
import matplotlib.pyplot as plt
plt.plot(x, marker='*')
plt.show()
沿梯度(斜率)的反方向移动,这就是“梯度下降法”。如上图所示,不管初始化值设为什么,在迭代过程只会越来越接近目标值,而不会偏离目标值,这就是梯度下降法的魅力。 上面这张图是表示的是一个一元函数搜索极值的问题,未必能很好展示梯度下降法的魅力,你再返回去看上面那张“势能梯度图”,那是一个二元函数搜索极值的过程。左边的搜索路径很简洁,而右边的搜索路径,尽管因为初始值的设定,导致它的路径很曲折,但是,你有没有发现,它的每一次迭代事实上离目标都更近一步。我想,这就是梯度下降法的优点吧! 注:这段代码是一元函数求极值,如果是二元函数,则需要同时满足两个分量的偏导数的值为零,下面的线性回归程序算的就是二元偏导数。
通过组合最小二乘法和梯度下降法,你可以得到线性回归,如下:
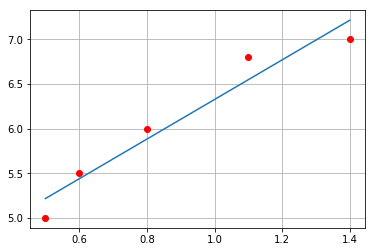
# Price of wheat/kg and the average price of bread
wheat_and_bread = [[0.5,5],[0.6,5.5],[0.8,6],[1.1,6.8],[1.4,7]]
def step_gradient(b_current, m_current, points, learningRate):
b_gradient = 0
m_gradient = 0
N = float(len(points))
for i in range(0, len(points)):
x = points[i][0]
y = points[i][1]
b_gradient += -(2/N) * (y -((m_current * x) + b_current))
m_gradient += -(2/N) * x * (y -((m_current * x) + b_current))
new_b = b_current -(learningRate * b_gradient)
new_m = m_current -(learningRate * m_gradient)
return [new_b, new_m]
def gradient_descent_runner(points, starting_b, starting_m, learning_rate, num_iterations):
b = starting_b
m = starting_m
for i in range(num_iterations):
b, m = step_gradient(b, m, points, learning_rate)
return [b, m]
gradient_descent_runner(wheat_and_bread, 1, 1, 0.01, 1000)
# [3.853945094921183, 2.4895803107016445]
上面这个程序的核心思想就是:在内层迭代的过程中,算出每一步误差函数相当于 m 和 b 的偏导数(梯度),然后沿梯度的反方向调整 m 和 b ;外层迭代执行梯度下降法,逐步逼近偏导数等于0的点。 其中需要注意偏导数的近似计算公式,已知误差函数
即各点与拟合直线的距离的平方和,再做算术平均。然后可以计算偏导数为
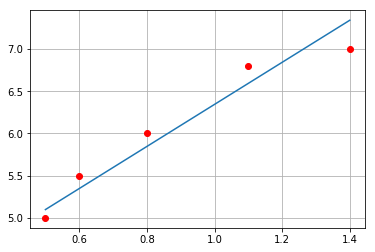
其中的求和公式在程序中表现为内层for循环 下面再给出拟合后的效果图
import numpy as np
import matplotlib.pyplot as plt
a = np.array(wheat_and_bread)
plt.plot(a[:,0], a[:,1], 'ro')
b,m = gradient_descent_runner(wheat_and_bread, 1, 1, 0.01, 1000)
x = np.linspace(a[0,0], a[-1,0])
y = m * x + b
plt.plot(x, y)
plt.grid()
plt.show()
对比 Numpy
import numpy as np
import matplotlib.pyplot as plt
a = np.array(wheat_and_bread)
plt.plot(a[:,0], a[:,1], 'ro')
m, b = np.polyfit(a[:,0], a[:,1], 1)
print([b,m])
x = np.linspace(a[0,0], a[-1,0])
y = m * x + b
plt.plot(x, y)
plt.grid()
plt.show()
# [4.1072992700729891, 2.2189781021897814]