支持向量机

1. sklearn.svm.SVC 参数、属性和接口

class sklearn.svm.SVC (C=1.0, kernel=’rbf’, degree=3,
                        gamma=’auto_deprecated’, coef0=0.0, shrinking=True,
                        probability=False, tol=0.001, cache_size=200, 
                        class_weight=None, verbose=False, max_iter=-1,
                        decision_function_shape=’ovr’, random_state=None
                    )

参数

• C ：浮点数，默认1，必须大于等于0，可不填 松弛系数的惩罚项系数。如果 C 值设定比较大，那 SVC 可能会选择边际较小的，能够更好地分类所有训 练点的决策边界，不过模型的训练时间也会更长。如果 C 的设定值较小，那 SVC 会尽量最大化边界，决 策功能会更简单，但代价是训练的准确度。换句话说，C 在 SVM 中的影响就像正则化参数对逻辑回归的 影响

• kernel ：核函数，默认是 rbf，可以是 linear , poly , rbf, sigmoid, precomputed

  

• degree ：整数，可不填，默认3, 多项式核函数的次数（poly），如果核函数没有选择poly，这个参数会被忽略

• gamma ： 浮点数，可不填，默认auto 核函数的系数，仅在参数Kernel的选项为rbf,poly和sigmoid的时候有效

  • 输入auto，自动使用1/(n_features)作为gamma的取值
  • 输入scale，则使用1/(n_features * X.std())作为gamma的取值
  • 输入auto_deprecated，则表示没有传递明确的gamma值（不推荐使用）

• coef0 ：浮点数，可不填，默认=0.0 核函数中的常数项，它只在参数kernel为poly和sigmoid的时候有效

  选取与核函数相关的参数：degree & gamma & coef0

  

主要调节的参数有：C 、kernel 、degree 、gamma 、coef0 。

clf = SVC(kernel = "linear")

重要属性 :

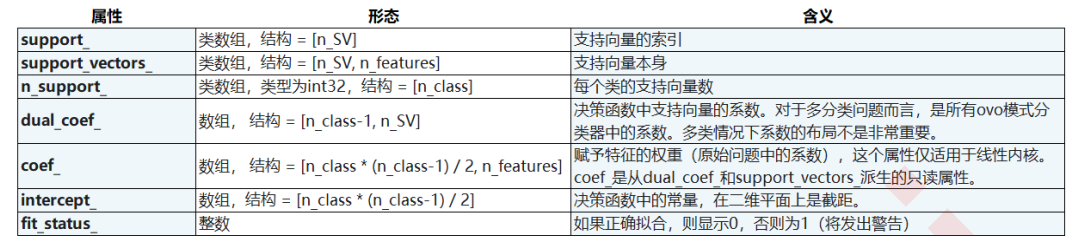
SVC的接口列表 ：

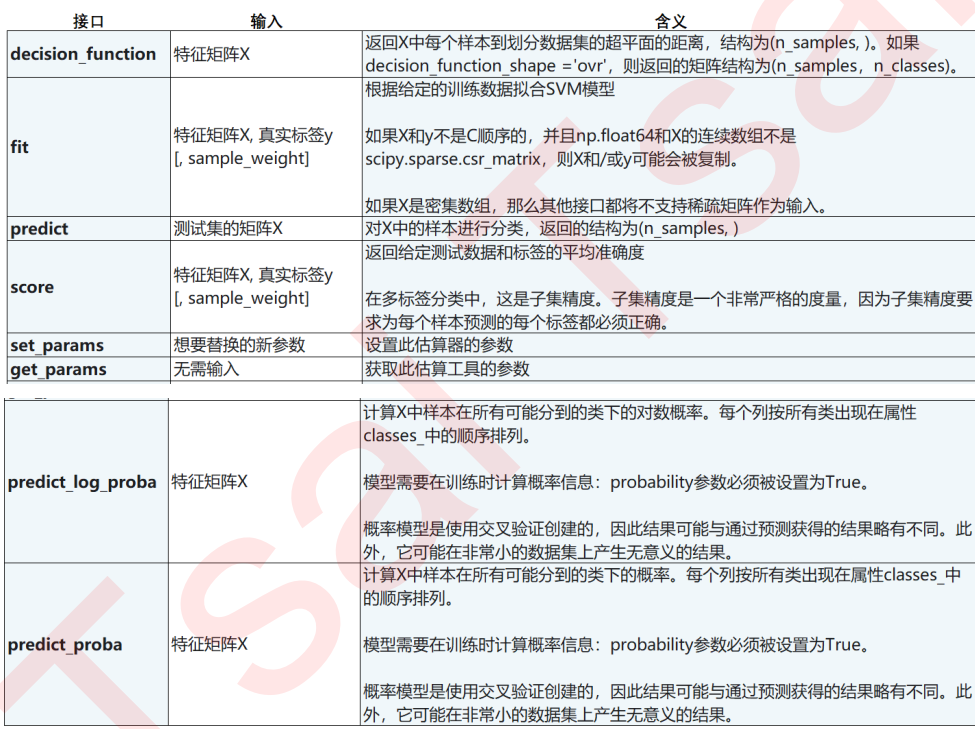
2. 二分类SVC中的样本不均衡问题：重要参数class_weight

首先，分类模型天生会倾向于多数的类，让多数类更容易被判断正确，少数类被牺牲掉。因为对于模型而言，样本量越大的标签可以学习的信息越多，算法就会更加依赖于从多数类中学到的信息来进行判断。如果我们希望捕获少数类，模型就会失败。其次，模型评估指标会失去意义。这种分类状况下，即便模型什么也不做，全把所有人都当成不会犯罪的人，准确率也能非常高，这使得模型评估指标accuracy变得毫无意义，根本无法达到我们的“要识别出会犯罪的人”的建模目的。 所以现在，我们首先要让算法意识到数据的标签是不均衡的，通过施加一些惩罚或者改变样本本身，来让模型向着捕获少数类的方向建模。然后，我们要改进我们的模型评估指标，使用更加针对于少数类的指标来优化模型

在支持向量机中，我们要大力依赖我们调节样本均衡的参数：SVC类中的class_weight和接口fit中可以设定的sample_weight.

2.1 SVC 的参数：class_weight

可输入字典或者balanced，可不填，默认None 对SVC，将类 i 的参数 C 设置为class_weight [i] * C。

如果没有给出具体的 class_weight，则所有类都被假设为占有相同的权重1，模型会根据数据原本的状况去训练。如果希望改善样本不均衡状况，请输入形如{"标签的值1"：权重1，"标签的值2"：权重2}的字典，则参数C将会自动被设为：标签的值1的C：权重1 C，标签的值2的C：权重2C 或者，可以使用“balanced”模式，这个模式使用y的值自动调整与输入数据中的类频率成反比的权重为 n_samples/(n_classes * np.bincount(y))

2.2 SVC 的接口fit 的参数：sample_weight

数组，结构为 (n_samples )，必须对应输入fit中的特征矩阵的每个样本

每个样本在 fit 时的权重，让权重 每个样本对应的C值来迫使分类器强调设定的权重更大的样本。通常，较大的权重加在少数类的样本上，以迫使模型向着少数类的方向建模

通常来说，这两个参数我们只选取一个来设置。如果我们同时设置了两个参数，则C会同时受到两个参数的影响，即 class_weight 中设定的权重 sample_weight中设定的权重 C

3. 重要参数probability，接口predict_proba以及decision_function

我们在SVM中利用超平面来判断我们的样本，本质上来说，当两个点的距离是相同的符号的时候，越远离超平面的样本点归属于某个标签类的概率就很大。比如说，一个距离超平面0.1的点，和一个距离超平面100的点，明显是距离为0.1的点更有可能是负类别的点混入了边界。同理，一个距离超平面距离为-0.1的点，和一个离超平面距离为-100的点，明显是-100的点的标签更有可能是负类。所以，到超平面的距离一定程度上反应了样本归属于某个标签类的可能性。接口decision_function返回的值也因此被我们认为是 SVM 中的置信度（confidence）

不过，置信度始终不是概率，它没有边界，可以无限大，大部分时候也不是以百分比或者小数的形式呈现，而 SVC 的判断过程又不像决策树一样可以求解出一个比例。为了解决这个矛盾，SVC有重要参数probability 布尔值，可不填，默认 False 是否启用概率估计。进行必须在调用fit之前启用它，启用此功能会减慢 SVM 的运算速度。设置为True则会启动，启用之后，SVC的接口predict_proba和predict_log_proba将生效 。

from sklearn.datasets import make_blobs
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np

class_1 = 500  # 类别1有500个样本
class_2 = 50  # 类别2只有50个
centers = [[0.0, 0.0], [2.0, 2.0]]  # 设定两个类别的中心
clusters_std = [1.5, 0.5]  # 设定两个类别的方差，通常来说，样本量比较大的类别会更加松散
X, y = make_blobs(n_samples=[class_1, class_2],
                  centers=centers,
                  cluster_std=clusters_std,
                  random_state=0, shuffle=False)

#看看数据集长什么样
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="rainbow",s=10)
#其中红色点是少数类，紫色点是多数类

clf_proba.predict_proba(X) # 生成的各类标签下的概率

clf_proba.predict_proba(X).shape

clf_proba.decision_function(X) # 样本到决策边界的距离

clf_proba.decision_function(X).shape

在二分类过程中，decision_function只会生成一列距离，样本的类别由距离的符号来判断，但是 predict_proba会生成两个类别分别对应的概率。SVM 也可以生成概率，所以我们可以使用和逻辑回归同样的方式来在 SVM 上设定和调节我们的阈值。

在二分类过程中，有可能出现predict_proba返回的概率小于0.5，但样本依旧被标记为正类的情况出现，毕竟支持向量机本身并不依赖于概率来完成自己的分类。如果我们的确需要置信度分数，但不一定非要是概率形式的话，那建议可以将probability设置为False，使用decision_function这个接口而不是predict_proba .

重要概念

决策边界是比所在数据空间小一维的空间，在三维数据空间中就是一个平面，在二维数据空间中就是一条直线