逻辑回归
理解逻辑回归,必须要有一定的数学基础,必须理解损失函数,正则化,梯度下降,海森矩阵等等这些复杂的概念,才能够对逻辑回归进行调优
概率,研究的是自变量和因变量之间的关系
似然,研究的是参数取值与因变量之间的关系
sklearn 中的逻辑回归
| 逻辑回归相关的类 | 说明 |
|---|---|
| linear_model.LogisticRegression | 逻辑回归分类器(又叫logit回归,最大熵分类器) |
| linear_model.LogisticRegressionCV | 带交叉验证的逻辑回归分类器 |
| linear_model.logistic_regression_path | 计算Logistic回归模型以获得正则化参数的列表 |
| linear_model.SGDClassifier | 利用梯度下降求解的线性分类器(SVM,逻辑回归等等) |
| linear_model.SGDRegressor | 利用梯度下降最小化正则化后的损失函数的线性回归模型 |
1. linear_model.LogisticRegression
class sklearn.linear_model.LogisticRegression (penalty=’l2’, dual=False,
tol=0.0001, C=1.0,
fit_intercept=True, intercept_scaling=1,
class_weight=None, random_state=None,
solver=’warn’, max_iter=100,
multi_class=’warn’, verbose=0,
warm_start=False, n_jobs=None
)
参数:




L1正则化和L2正则化虽然都可以控制过拟合,但它们的效果并不相同。当正则化强度逐渐增大(即C逐渐变小), 参数 的取值会逐渐变小,但L1正则化会将参数压缩为0,L2正则化只会让参数尽量小,不会取到0
在L1正则化在逐渐加强的过程中,携带信息量小的、对模型贡献不大的特征的参数,会比携带大量信息的、对模型有巨大贡献的特征的参数更快地变成0,所以L1正则化本质是一个特征选择的过程,掌管了参数的“稀疏性”。L1正 则化越强,参数向量中就越多的参数为0,参数就越稀疏,选出来的特征就越少,以此来防止过拟合。因此,如果特征量很大,数据维度很高,我们会倾向于使用L1正则化 ,相对的,L2正则化在加强的过程中,会尽量让每个特征对模型都有一些小的贡献,但携带信息少,对模型贡献不大的特征的参数会非常接近于0。通常来说,如果我们的主要目的只是为了防止过拟合,选择L2正则化就足够了。但是如果选择L2正则化后还是过拟合,模型在未知数据集上的效果表现很差,就可以考虑L1正则化。
属性列表:

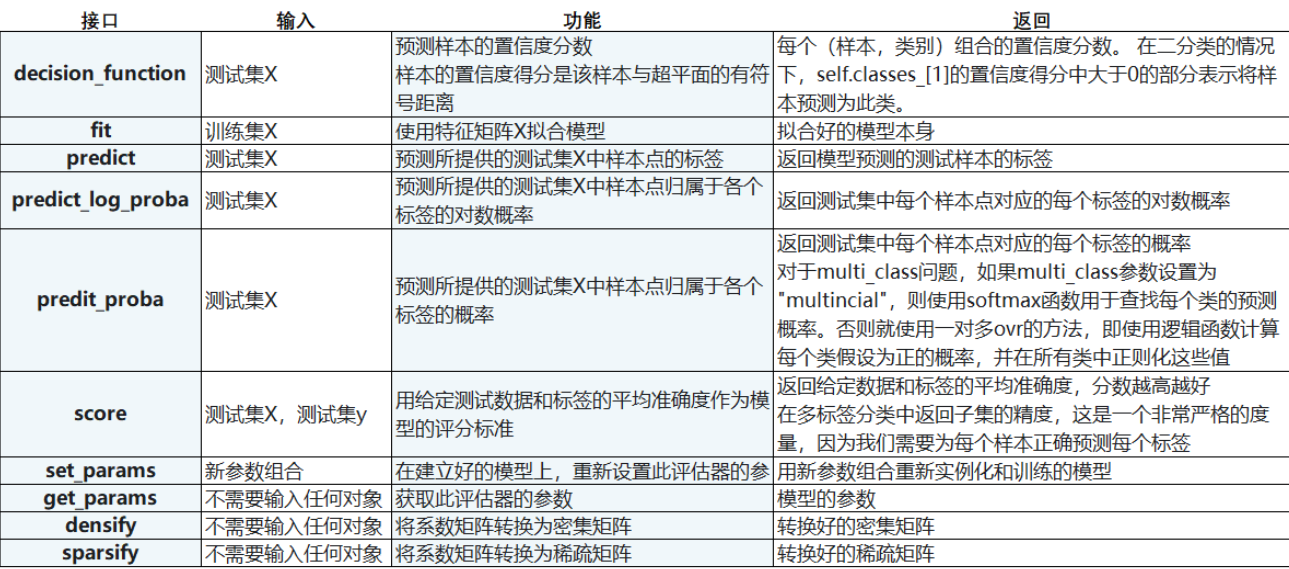
接口列表