sklearn.metrics.roc_curve用法
ROC 是一条以不同阈值下的假正率 FPR 为横坐标,不同阈值下的召回率 Recall 为纵坐标的曲线。
建立 ROC 曲线的根本目的是找寻 Recall 和 FPR 之间的平衡,让我们能够衡量模型在尽量捕捉少数类的时候,误伤多数类的情况会如何变化。横坐标是FPR,代表着模型将多数类判断错误的能力,纵坐标Recall,代表着模型捕捉少数类的能力,所以ROC曲线代表着,随着Recall的不断增加,FPR如何增加。我们希望随着Recall的不断提升,FPR增加得越慢越好,这说明我们可以尽量高效地捕捉出少数类,而不会将很多地多数类判断错误
sklearn.metrics.roc_curve ( y_true,
y_score,
pos_label=None,
sample_weight=None,
drop_intermediate=True
)
参数:
y_true: 数组,形状 = [n_samples],真实标签y_score: 数组,形状 = [n_samples],置信度分数,可以是正类样本的概率值,或置信度分数,或者SVC中decision_function返回的距离pos_label: 整数或者字符串, 默认None,表示被认为是正类样本的类别 . 即标签中认定为正的label个数。例如label= [1,2,3,4],如果设置pos_label = 2,则认为3,4为positive,其他均为negtive。
sample_weight: 形如 [n_samples]的类数组结构,可不填,表示样本的权重drop_intermediate: 布尔值,默认True,如果设置为True,表示会舍弃一些ROC曲线上不显示的阈值点,这对于计算一个比较轻量的ROC曲线来说非常有用
返回值:
FPR,Recall以及阈值。
Example 1
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import roc_curve
class_1 = 500 # 类别1有500个样本
class_2 = 50 # 类别2只有50个
centers = [[0.0, 0.0], [2.0, 2.0]] # 设定两个类别的中心
clusters_std = [1.5, 0.5] # 设定两个类别的方差,通常来说,样本量比较大的类别会更加松散
X, y = make_blobs(n_samples=[class_1, class_2],
centers=centers,
cluster_std=clusters_std,
random_state=0, shuffle=False)
#看看数据集长什么样
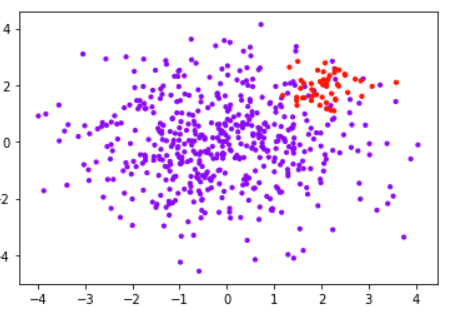
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="rainbow",s=10)
#其中红色点是少数类,紫色点是多数类
clf_proba = SVC(kernel="linear",C=1.0,probability=True).fit(X,y)
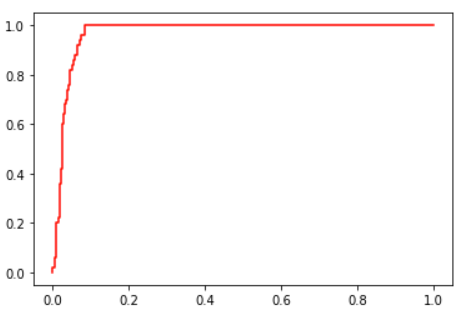
FPR, recall, thresholds = roc_curve(y,clf_proba.decision_function(X), pos_label=1)
plt.plot(FPR, recall, color='red',label='ROC curve (area = %0.2f)' )
Example 2
初始数据:
y_true = [0, 0, 1, 0, 0, 1, 0, 1, 0, 0]
y_score = [0.31689620142873609, 0.32367439192936548, 0.42600526758001989, 0.38769987193780364, 0.3667541015524296, 0.39760831479768338, 0.42017521636505745, 0.41936155918127238, 0.33803961944475219, 0.33998332945141224]
通过sklearn的roc_curve函数计算false positive rate和true positive rate以及对应的threshold:
fpr, tpr, thresholds = roc_curve(y_true,
y_score,
drop_intermediate=False)
计算得到的值如下:
fpr
array([0. , 0. , 0.14285714, 0.14285714, 0.14285714,
0.28571429, 0.42857143, 0.57142857, 0.71428571, 0.85714286,
1. ])
tpr
array([0. , 0.33333333, 0.33333333, 0.66666667, 1. ,
1. , 1. , 1. , 1. , 1. ,
1. ])
thresholds
array([1.42600527, 0.42600527, 0.42017522, 0.41936156, 0.39760831,
0.38769987, 0.3667541 , 0.33998333, 0.33803962, 0.32367439,
0.3168962 ])