线性回归
sklearn中的线性模型模块是linear_model,我们曾经在学习逻辑回归的时候提到过这个模块。linear_model包含了多种多样的类和函数,其中逻辑回归相关的类和函数在这里就不给大家列举了。今天的课中我将会为大家来讲解:普通线性回归,多项式回归,岭回归,LASSO,以及弹性网 。
| 类/函数 | 含义 |
|---|---|
| linear_model.LinearRegression | 使用普通最小二乘法的线性回归 |
| 岭回归 | |
| linear_model.Ridge | 岭回归,一种将 L2 作为正则化工具的线性最小二乘回归 |
| LASSO | |
| linear_model.Lasso | Lasso,使用L1作为正则化工具来训练的线性回归模型 |
多元线性回归LinearRegression
class sklearn.linear_model.LinearRegression(fit_intercept=True,
normalize=False,
copy_X=True,
n_jobs=None
)
参数
| 参数 | 含义 |
|---|---|
| fit_intercept | 布尔值,可不填,默认为True 是否计算此模型的截距。如果设置为False,则不会计算截距 |
| normalize | 布尔值,可不填,默认为False 当fit_intercept设置为False时,将忽略此参数。如果为True,则特征矩阵X在进入回归之前将 会被减去均值(中心化)并除以L2范式(缩放)。如果你希望进行标准化,请在fit数据之前 使用preprocessing模块中的标准化专用类StandardScaler |
| copy_X | 布尔值,可不填,默认为True 如果为真,将在X.copy()上进行操作,否则的话原本的特征矩阵X可能被线性回归影响并覆盖 |
| n_jobs | 整数或者None,可不填,默认为None 用于计算的作业数。只在多标签的回归和数据量足够大的时候才生效。除非None在 joblib.parallel_backend上下文中,否则None统一表示为1。如果输入 -1,则表示使用全部 的CPU来进行计算。 |
属性
| 属性 | 含义 |
|---|---|
| coef_ | 数组,形状为 (n_features, )或者(n_targets, n_features) 线性回归方程中估计出的系数。如果在fit中传递多个标签(当y为二维或以上的时候),则返回 的系数是形状为(n_targets,n_features)的二维数组,而如果仅传递一个标签,则返回的系 数是长度为n_features的一维数组 |
| intercept_ | 数组,线性回归中的截距项。 |
linear_model.Ridge
class sklearn.linear_model.Ridge(alpha=1.0,
fit_intercept=True,
normalize=False,
copy_X=True,
max_iter=None,
tol=0.001,
solver='auto',
random_state=None
)
和线性回归相比,岭回归的参数稍微多了那么一点点,但是真正核心的参数就是我们的正则项的系数 ,其他的参数是当我们希望使用最小二乘法之外的求解方法求解岭回归的时候才需要的,通常我们完全不会去触碰这些参数。所以大家只需要了解 的用法就可以了
非线性问题:多项式回归
对于回归问题,数据若能分布为一条直线,则是线性的,否则是非线性。对于分类问题,数据分布若能使用一条直线来划分类别,则是线性可分的,否则数据则是线性不可分的 。
线性模型与非线性模型
在回归中,线性数据可以使用如下的方程来进行拟合 :
也就是我们的线性回归的方程。根据线性回归的方程,我们可以拟合出一组参数 ,在这一组固定的参数下我们可以建立一个模型,而这个模型就被我们称之为是线性回归模型。所以建模的过程就是寻找参数的过程。此时此刻我们建立的线性回归模型,是一个用于拟合线性数据的线性模型。作为线性模型的典型代表,我们可以从线性回归的方程中总结出线性模型的特点:其自变量都是一次项。
多项式回归PolynomialFeatures
class sklearn.preprocessing.PolynomialFeatures (degree=2,
interaction_only=False,
include_bias=True
)
| 参数 | 含义 |
|---|---|
| degree | 多项式中的次数,默认为2 |
| interaction_only | 布尔值是否只产生交互项,默认为False |
| include_bias | 布尔值,是否产出与截距项相乘的 ,默认True |
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
#如果原始数据是一维的
X = np.arange(1,4).reshape(-1,1)
X #
二次多项式,参数degree控制多项式的次方
poly = PolynomialFeatures(degree=2)
#接口transform直接调用
X_ = poly.fit_transform(X)
X_
X_.shape
#三次多项式
PolynomialFeatures(degree=3).fit_transform(X)
多项式变化后数据看起来不太一样了:首先,数据的特征(维度)增加了,这正符合我们希望的将数据转换到高维空间的愿望。其次,维度的增加是有一定的规律的。不难发现,如果我们本来的特征矩阵中只有一个特征 ,而转换后我们得到:

这个规律在转换为二次多项式的时候同样适用。原本,我们的模型应该是形似 的结构,而转换后我们的特征变化导致了模型的变化。根据我们在支持向量机中的经验,现在这个被投影到更高维空间中的数据在某个角度上看起来已经是一条直线了,于是我们可以继续使用线性回归来进行拟合。线性回归是会对每个特征拟合出权重 的,所以当我们拟合高维数据的时候,我们会得到下面的模型
由此推断,假设多项式转化的次数是n,则数据会被转化成形如:
而拟合出的方程也可以被改写成:
这个过程看起来非常简单,只不过是将原始的 上的次方增加,并且为这些次方项都加上权重 ,然后增加一列所有次方为0的列作为截距乘数的 ,参数include_bias就是用来控制 的生成的 .
#三次多项式,不带与截距项相乘的x0
PolynomialFeatures(degree=3,include_bias=False).fit_transform(X)
#为什么我们会希望不生成与截距相乘的x0呢?
#对于多项式回归来说,我们已经为线性回归准备好了x0,但是线性回归并不知道
xxx = PolynomialFeatures(degree=3).fit_transform(X)
xxx.shape
rnd = np.random.RandomState(42) #设置随机数种子
y = rnd.randn(3)
y #
生成了多少个系数?
LinearRegression().fit(xxx,y).coef_
#查看截距
LinearRegression().fit(xxx,y).intercept_
#发现问题了吗?线性回归并没有把多项式生成的x0当作是截距项
#所以我们可以选择:关闭多项式回归中的include_bias
#也可以选择:关闭线性回归中的fit_intercept
#生成了多少个系数?
LinearRegression(fit_intercpet=False).fit(xxx,y).coef_
#查看截距
LinearRegression(fit_intercpet=False).fit(xxx,y).intercept_
不过,这只是一维状况的表达,大多数时候我们的原始特征矩阵不可能会是一维的,至少也是二维以上,很多时候还可能存在上千个特征或者维度。现在我们来看看原始特征矩阵是二维的状况:
X = np.arange(6).reshape(3, 2)
X #
尝试二次多项式
PolynomialFeatures(degree=2).fit_transform(X)
很明显,上面一维的转换公式已经不适用了,但如果我们仔细看,是可以看出这样的规律的 :
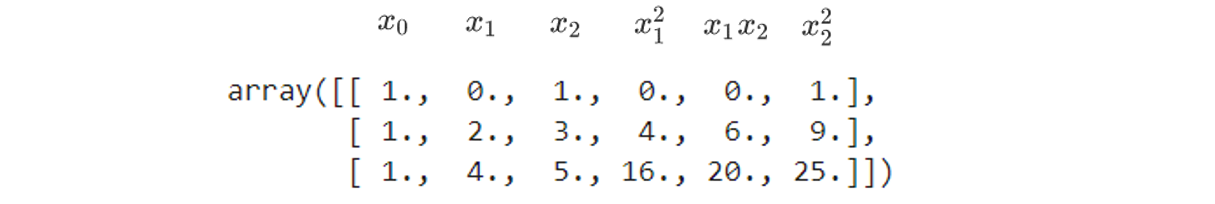
当原始特征为二维的时候,多项式的二次变化突然将特征增加到了六维,其中一维是常量(也就是截距)。当我们继续适用线性回归去拟合的时候,我们会得到的方程如下 :
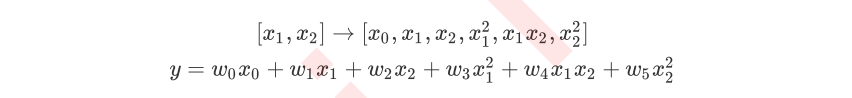
这个时候大家可能就会感觉到比较困惑了,怎么会出现这样的变化?如果想要总结这个规律,可以继续来尝试三次多项式
# 尝试三次多项式
PolynomialFeatures(degree=3).fit_transform(X)
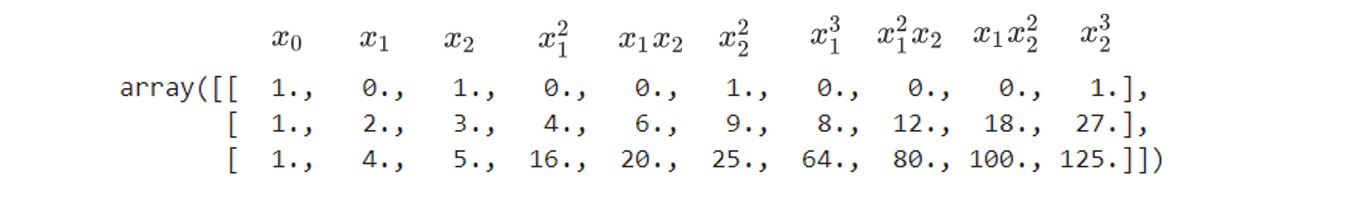
不难发现:当我们进行多项式转换的时候,多项式会产出到最高次数为止的所有低高次项
比如如果我们规定多项式的次数为2,多项式就会产出所有次数为1和次数为2的项反馈给我们,相应的如果我们规定多项式的次数为n,则多式会产出所有从次数为1到次数为n的项。注意 和 一样都是二次项,一个自变量的平方其实也就相当于是 ,所以在三次多项式中 就是三次项。
在多项式回归中,我们可以规定是否产生平方或者立方项,其实如果我们只要求高次项的话, 会是一个比 更好的高次项,因为 和之间的共线性会比与之间的共线性好那么一点点(只是一点点),而我们多项式转化之后是需要使用线性回归模型来进行拟合的,就算机器学习中不是那么在意数据上的基本假设,但是太过分的共线性还是会影响到模型的拟合。
因此sklearn中存在着控制是否要生成平方和立方项的参数interaction_only,默认为 False,以减少共线性 。
PolynomialFeatures(degree=2).fit_transform(X)
PolynomialFeatures(degree=2,interaction_only=True).fit_transform(X)
#对比之下,当interaction_only为True的时候,只生成交互项
随着多项式的次数逐渐变高,特征矩阵会被转化得越来越复杂。不仅是次数,当特征矩阵中的维度数(特征数)增加的时候,多项式同样会变得更加复杂 :
#更高维度的原始特征矩阵
X = np.arange(9).reshape(3, 3)
X
PolynomialFeatures(degree=2).fit_transform(X)
PolynomialFeatures(degree=3).fit_transform(X)
X_ = PolynomialFeatures(degree=20).fit_transform(X)
X_.shape
多项式变化对于数据会有怎样的影响:随着原特征矩阵的维度上升,随着我们规定的最高次数的上升,数据会变得越来越复杂,维度越来越多,并且这种维度的增加并不能用太简单的数学公式表达出来。因此,多项式回归没有固定的模型表达式,多项式回归的模型最终长什么样子是由数据和最高次数决定的,因此我们无法断言说某个数学表达式"就是多项式回归的数学表达",因此要求解多项式回归不是一件容易的事儿 。