朴素贝叶斯
sklearn中的朴素贝叶斯
| 类 | 含义 |
|---|---|
| naive_bayes.GaussianNB | 高斯分布下的朴素贝叶斯 |
| naive_bayes.BernoulliNB | 伯努利分布下的朴素贝叶斯 |
| naive_bayes.MultinomialNB | 多项式分布下的朴素贝叶斯 |
| naive_bayes.ComplementNB | 补集朴素贝叶斯 |
1. 高斯朴素贝叶斯 GaussianNB
class sklearn.naive_bayes.GaussianNB (priors=None, var_smoothing=1e-09)
参数:
- prior :可输入任何类数组结构,形状为(n_classes,) 表示类的先验概率。如果指定,则不根据数据调整先验,如果不指定,则自行根据数据计 算先验概率 $P(Y)$
- var_smoothing : 浮点数,可不填(默认值= 1e-9) 在估计方差时,为了追求估计的稳定性,将所有特征的方差中最大的方差以某个比例添加 到估计的方差中。这个比例,由var_smoothing参数控制
Examples:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
digits = load_digits() #手写数据集
X, y = digits.data, digits.target
# 划分数据集
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
np.unique(Ytrain) #多分类问题,类别是10个
gnb = GaussianNB().fit(Xtrain,Ytrain)
#查看分数
acc_score = gnb.score(Xtest,Ytest) #返回预测的精确性 accuracy
#查看预测结果
Y_pred = gnb.predict(Xtest)
#查看预测的概率结果
prob = gnb.predict_proba(Xtest)
prob.shape #每一列对应一个标签类别下的概率
# (540, 10)
使用混淆矩阵来查看贝叶斯的分类结果
from sklearn.metrics import confusion_matrix as CM
CM(Ytest,Y_pred)
#注意,ROC曲线是不能用于多分类的。多分类状况下最佳的模型评估指标是混淆矩阵和整体的准确度
#array([[47, 0, 0, 0, 0, 0, 0, 1, 0, 0],
# [ 0, 46, 2, 0, 0, 0, 0, 3, 6, 2],
# [ 0, 2, 35, 0, 0, 0, 1, 0, 16, 0],
# [ 0, 0, 1, 40, 0, 1, 0, 3, 4, 0],
# [ 0, 0, 1, 0, 39, 0, 1, 4, 0, 0],
# [ 0, 0, 0, 2, 0, 58, 1, 1, 1, 0],
# [ 0, 0, 1, 0, 0, 1, 49, 0, 0, 0],
# [ 0, 0, 0, 0, 0, 0, 0, 54, 0, 0],
# [ 0, 3, 0, 1, 0, 0, 0, 2, 55, 0],
# [ 1, 1, 0, 1, 2, 0, 0, 3, 7, 41]], dtype=int64)
2. 多项式朴素贝叶斯 MultinomialNB
多项式贝叶斯可能是除了高斯之外,最为人所知的贝叶斯算法了。它也是基于原始的贝叶斯理论,但假设概率分布是服从一个简单多项式分布。多项式分布来源于统计学中的多项式实验,这种实验可以具体解释为:实验包括n次重复试验,每项试验都有不同的可能结果。在任何给定的试验中,特定结果发生的概率是不变的。
- 多项式分布擅长的是分类型变量
- 多项式实验中的实验结果都很具体,它所涉及的特征往往是次数,频率,计数,出现与否这样的概念,这些概念都是离散的正整数,因此sklearn中的多项式朴素贝叶斯不接受负值的输入 。
由于这样的特性,多项式朴素贝叶斯的特征矩阵经常是稀疏矩阵(不一定总是稀疏矩阵),并且它经常被用于文本分类
多项式模型在计算先验概率 和条件概率 时,会做一些平滑处理,具体公式为:
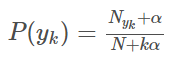
N是总的样本个数,k是总的类别个数, 是类别为 的样本个数, 是平滑值。
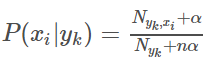
是类别为 的样本个数,n是特征的维数, 是类别为 的样本中,第 维特征的值是 的样本个数, 是平滑值。
在sklearn中,用来执行多项式朴素贝叶斯的类MultinomialNB包含如下的参数和属性 。
class sklearn.naive_bayes.MultinomialNB (alpha=1.0, fit_prior=True, class_prior=None)
参数:
alpha : 浮点数, 可不填 (默认为1.0)
拉普拉斯或利德斯通平滑的参数 ,如果设置为0则表示完全没有平滑选项。但是需要注意的是,平滑相当于人 为给概率加上一些噪音,因此 $\alpha$ 设置得越大,多项式朴素贝叶斯的精确性会越低(虽然影响不是非常大),布里 尔分数也会逐渐升高
fit_prior : 布尔值, 可不填 (默认为True)
是否学习先验概率 。如果设置为false,则不使用先验概率,而使用统一先验概率(uniform prior),即认为每个标签类出现的概率是 1 / n_classes
class_prior:形似数组的结构,结构为(n_classes, ),可不填(默认为None)
类的先验概率 。如果没有给出具体的先验概率则自动根据数据来进行计算
Examples:
导入需要的模块和库
from sklearn.preprocessing import MinMaxScaler
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_blobs
from sklearn.metrics import brier_score_los
建立数据集
class_1 = 500
class_2 = 500 #两个类别分别设定500个样本
centers = [[0.0, 0.0], [2.0, 2.0]] #设定两个类别的中心
clusters_std = [0.5, 0.5] #设定两个类别的方差
X, y = make_blobs(n_samples=[class_1, class_2],
centers=centers,
cluster_std=clusters_std,
random_state=0, shuffle=False
)
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y
,test_size=0.3
,random_state=420
)
归一化,确保输入的矩阵不带有负数
#先归一化,保证输入多项式朴素贝叶斯的特征矩阵中不带有负数
mms = MinMaxScaler().fit(Xtrain)
Xtrain_ = mms.transform(Xtrain)
Xtest_ = mms.transform(Xtest)
建立一个多项式朴素贝叶斯分类器
mnb = MultinomialNB().fit(Xtrain_, Ytrain)
#重要属性:调用根据数据获取的,每个标签类的对数先验概率log(P(Y))
#由于概率永远是在[0,1]之间,因此对数先验概率返回的永远是负值
mnb.class_log_prior_
# 两类的先验概率
# array([-0.69029411, -0.69600841])
mnb.class_log_prior_.shape
np.unique(Ytrain)
# array([0, 1])
#可以使用np.exp来查看真正的概率值
np.exp(mnb.class_log_prior_)
# 两类的概率值
# array([0.50142857, 0.49857143])
#重要属性:返回一个固定标签类别下的每个特征的对数概率log(P(Xi|y))
mnb.feature_log_prob_
# array([[-0.76164788, -0.62903951],
# [-0.72500918, -0.6622691 ]])
mnb.feature_log_prob_.shape
# 2 个特征,2 个标签
# (2, 2)
#重要属性:在fit时每个标签类别下包含的样本数。当fit接口中的sample_weight被设置时,
#该接口返回的值也会受到加权的影响
mnb.class_count_
# 每个类别样本的数量
#array([351., 349.])
mnb.class_count_.shape
分类器的效果如何呢?
#一些传统的接口
mnb.predict(Xtest_)
mnb.predict_proba(Xtest_)
mnb.score(Xtest_,Ytest)
# 0.5433333333333333
效果不太理想
#来试试看把Xtiain转换成分类型数据吧
#注意我们的Xtrain没有经过归一化,因为做哑变量之后自然所有的数据就不会又负数了
from sklearn.preprocessing import KBinsDiscretizer
kbs = KBinsDiscretizer(n_bins=10, encode='onehot').fit(Xtrain)
Xtrain_ = kbs.transform(Xtrain)
Xtest_ = kbs.transform(Xtest)
mnb = MultinomialNB().fit(Xtrain_, Ytrain)
mnb.score(Xtest_,Ytest)
# 0.9966666666666667
可以看出,多项式朴素贝叶斯的基本操作和代码都非常简单。同样的数据,如果采用哑变量方式的分箱处理,多项式贝叶斯的效果会突飞猛进
3. 伯努利朴素贝叶斯 BernoulliNB
多项式朴素贝叶斯可同时处理二项分布(抛硬币)和多项分布(掷骰子),其中二项分布又叫做伯努利分布,它是一种现实中常见,并且拥有很多优越数学性质的分布。因此,既然有着多项式朴素贝叶斯,我们自然也就又专门用来处理二项分布的朴素贝叶斯:伯努利朴素贝叶斯。
伯努利贝叶斯类BernoulliN假设数据服从多元伯努利分布,并在此基础上应用朴素贝叶斯的训练和分类过程。多元伯努利分布简单来说,就是数据集中可以存在多个特征,但每个特征都是二分类的,可以以布尔变量表示,也可以表示为{0,1}或者{-1,1}等任意二分类组合。因此,这个类要求将样本转换为二分类特征向量,如果数据本身不是二分类的,那可以使用类中专门用来二值化的参数binarize来改变数据。
伯努利朴素贝叶斯与多项式朴素贝叶斯非常相似,都常用于处理文本分类数据。但由于伯努利朴素贝叶斯是处理二项分布,所以它更加在意的是“存在与否”,而不是“出现多少次”这样的次数或频率,这是伯努利贝叶斯与多项式贝叶斯的根本性不同。在文本分类的情况下,伯努利朴素贝叶斯可以使用单词出现向量(而不是单词计数向量)来训练分类器。文档较短的数据集上,伯努利朴素贝叶斯的效果会更加好
class sklearn.naive_bayes.BernoulliNB (alpha=1.0, binarize=0.0,
fit_prior=True, class_prior=None)
参数:
alpha : 浮点数, 可不填 (默认为1.0)
拉普拉斯或利德斯通平滑的参数 ,如果设置为0则表示完全没有平滑选项。但是需要注意的是,平滑相当于人 为给概率加上一些噪音,因此 设置得越大,多项式朴素贝叶斯的精确性会越低(虽然影响不是非常大),布里 尔分数也会逐渐升高
binarize : 浮点数或None,可不填,默认为0
将特征二值化的阈值,如果设定为None,则会假定说特征已经被二值化完毕
fit_prior : 布尔值, 可不填 (默认为True)
是否学习先验概率 。如果设置为false,则不使用先验概率,而使用统一先验概率(uniform prior),即认为每个标签类出现的概率是 1 / n_classes.
class_prior:形似数组的结构,结构为(n_classes, ),可不填(默认为None)
类的先验概率 。如果没有给出具体的先验概率则自动根据数据来进行计算。
Examples:
from sklearn.naive_bayes import BernoulliNB
#普通来说我们应该使用二值化的类sklearn.preprocessing.Binarizer来将特征一个个二值化
#然而这样效率过低,因此我们选择归一化之后直接设置一个阈值
mms = MinMaxScaler().fit(Xtrain)
Xtrain_ = mms.transform(Xtrain)
Xtest_ = mms.transform(Xtest)
#不设置二值化
bnl_ = BernoulliNB().fit(Xtrain_, Ytrain)
bnl_.score(Xtest_,Ytest)
brier_score_loss(Ytest,bnl_.predict_proba(Xtest_)[:,1],pos_label=1)
#设置二值化阈值为0.5
bnl = BernoulliNB(binarize=0.5).fit(Xtrain_, Ytrain)
bnl.score(Xtest_,Ytest)
brier_score_loss(Ytest,bnl.predict_proba(Xtest_)[:,1],pos_label=1)
4. 补集朴素贝叶斯ComplementNB
补集朴素贝叶斯(complement naive Bayes,CNB)算法是标准多项式朴素贝叶斯算法的改进。CNB的发明小组创造出CNB的初衷是为了解决贝叶斯中的“朴素”假设带来的各种问题,他们希望能够创造出数学方法以逃避朴素贝叶斯中的朴素假设,让算法能够不去关心所有特征之间是否是条件独立的。以此为基础,他们创造出了能够解决样本不平衡问题,并且能够一定程度上忽略朴素假设的补集朴素贝叶斯。
在实验中,CNB的参数估计已经被证明比普通多项式朴素贝叶斯更稳定,并且它特别适合于样本不平衡的数据集。有时候,CNB在文本分类任务上的表现有时能够优于多项式朴素贝叶斯,因此现在补集朴素贝叶斯也开始逐渐流行
在sklearn中,补集朴素贝叶斯由类ComplementNB完成,它包含的参数和多项式贝叶斯也非常相似:
class sklearn.naive_bayes.ComplementNB (alpha=1.0, fit_prior=True,
class_prior=None, norm=False)
参数:
alpha : 浮点数, 可不填 (默认为1.0)
拉普拉斯或利德斯通平滑的参数 ,如果设置为0则表示完全没有平滑选项。但是需要注意的是,平滑相当于人 为给概率加上一些噪音,因此 $\alpha$ 设置得越大,多项式朴素贝叶斯的精确性会越低(虽然影响不是非常大),布里 尔分数也会逐渐升高
norm : 布尔值,可不填,默认False
在计算权重的时候是否适用L2范式来规范权重的大小。默认不进行规范,即不跟从补集朴素贝叶斯算法的全部 内容,如果希望进行规范,请设置为True
fit_prior : 布尔值, 可不填 (默认为True)
是否学习先验概率 。如果设置为false,则不使用先验概率,而使用统一先验概率(uniform prior),即认为每个标签类出现的概率是 1 / n_classes
class_prior:形似数组的结构,结构为(n_classes, ),可不填(默认为None)
类的先验概率 。如果没有给出具体的先验概率则自动根据数据来进行计算
Examples:
那来看看,补集朴素贝叶斯在不平衡样本上的表现吧,同时我们来计算一下每种贝叶斯的计算速度:
from sklearn.naive_bayes import ComplementNB
from time import time
import datetime
name = ["Multinomial","Gaussian","Bernoulli","Complement"]
models = [MultinomialNB(),GaussianNB(),BernoulliNB(),ComplementNB()]
for name,clf in zip(name,models):
times = time()
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y
,test_size=0.3
,random_state=420)
#预处理
if name != "Gaussian":
kbs = KBinsDiscretizer(n_bins=10, encode='onehot').fit(Xtrain)
Xtrain = kbs.transform(Xtrain)
Xtest = kbs.transform(Xtest)
clf.fit(Xtrain,Ytrain)
y_pred = clf.predict(Xtest)
proba = clf.predict_proba(Xtest)[:,1]
score = clf.score(Xtest,Ytest)
print(name)
print("\tBrier:{:.3f}".format(BS(Ytest,proba,pos_label=1)))
print("\tAccuracy:{:.3f}".format(score))
print("\tRecall:{:.3f}".format(recall_score(Ytest,y_pred)))
print("\tAUC:{:.3f}".format(AUC(Ytest,proba)))
print(datetime.datetime.fromtimestamp(time()-times).strftime("%M:%S:%f"))
输出:
Multinomial
Brier:0.007
Accuracy:0.990
Recall:0.000
AUC:0.991
00:00:050863
Gaussian
Brier:0.006
Accuracy:0.990
Recall:0.438
AUC:0.993
00:00:038898
Bernoulli
Brier:0.009
Accuracy:0.987
Recall:0.771
AUC:0.987
00:00:049866
Complement
Brier:0.038
Accuracy:0.953
Recall:0.987
AUC:0.991
00:00:044881