聚类算法K-Means

1. KMeans是如何工作的

2. sklearn.cluster.KMeans

class sklearn.cluster.KMeans (n_clusters=8, init=’k-means++’, 
                              n_init=10, max_iter=300, tol=0.0001,
                              precompute_distances=’auto’, 
                              verbose=0, random_state=None, 
                              copy_x=True, n_jobs=None, 
                              algorithm=’auto’
                             )

对于一个簇来说，所有样本点到质心的距离之和越小，我们就认为这个簇中的样本越相似，簇内差异就越小。而距离的衡量方法有多种，令 $x$ 表示簇中的一个样本点，$\mu$ 表示该簇中的质心，n表示每个样本点中的特征数目，i表示组成点 的每个特征，则该样本点到质心的距离可以由以下距离来度量：
$\text {欧几里得距离} d(x, \mu)=\sqrt{\sum_{i=1}^{n}\left(x_{i}-\mu_{i}\right)^{2}}$

$\text {曼哈顿距离}d(x, \mu)=\sum_{i=1}^{n}\left(\left|x_{i}-\mu\right|\right)$

$\text {余弦距离} \cos \theta=\frac{\sum_{1}^{n}\left(x_{i} * \mu\right)}{\sqrt{\sum_{1}^{n}\left(x_{i}\right)^{2}} * \sqrt{\sum_{1}^{n}(\mu)^{2}}}$

采用欧几里得距离，则一个簇中所有样本点到质心的距离的平方和为：
$\text { Cluster Sum of Square }(C S S)=\sum_{j=0}^{m} \sum_{i=1}^{n}\left(x_{i}-\mu_{i}\right)^{2}$

$\text {TotalCluster Sum of Square}=\sum_{l=1}^{k} C S S_{l}$

其中，m 为一个簇中样本的个数，j 是每个样本的编号。这个公式被称为簇内平方和（cluster Sum of Square），叫做 Inertia。而将一个数据集中的所有簇的簇内平方和相加，就得到了整体平方和（Total Cluster Sum of Square），又叫做 total inertia。Total Inertia 越小，代表着每个簇内样本越相似，聚类的效果就越好。因此 KMeans 追求的是，求解能够让 Inertia 最小化的质心

3. 重要参数

n_clusters

n_clusters是KMeans中的k，表示着我们告诉模型我们要分几类。这是KMeans当中唯一一个必填的参数，默认为8类，但通常我们的聚类结果会是一个小于8的结果

init & random_state & n_init

在K-Means中有一个重要的环节，就是放置初始质心。如果有足够的时间，K-means一定会收敛，但Inertia可能收敛到局部最小值。是否能够收敛到真正的最小值很大程度上取决于质心的初始化。init就是用来帮助我们决定初始化方式的参数。

初始质心放置的位置不同，聚类的结果很可能也会不一样，一个好的质心选择可以让K-Means避免更多的计算，让算法收敛稳定且更快。在之前讲解初始质心的放置时，我们是使用”随机“的方法在样本点中抽取k个样本作为初始质心，这种方法显然不符合”稳定且更快“的需求。为此，我们可以使用random_state参数来控制每次生成的初始质心都在相同位置，甚至可以画学习曲线来确定最优的random_state是哪个整数。

一个random_state对应一个质心随机初始化的随机数种子。如果不指定随机数种子，则sklearn中的K-means并不会只选择一个随机模式扔出结果，而会在每个随机数种子下运行多次，并使用结果最好的一个随机数种子来作为初始质心。我们可以使用参数n_init来选择，每个随机数种子下运行的次数。这个参数不常用到，默认10次，如果我们希望运行的结果更加精确，那我们可以增加这个参数n_init的值来增加每个随机数种子下运行的次数。
为了优化选择初始质心的方法 , 在sklearn中，我们使用参数 init ='k-means ++'来选择使用k-means ++作为质心初始化的方案

• init：可输入"k-means++"，"random"或者一个n维数组。这是初始化质心的方法，默认"k-means++"。输入"kmeans++"：一种为K均值聚类选择初始聚类中心的聪明的办法，以加速收敛。如果输入了n维数组，数组的形状应该是(n_clusters，n_features)并给出初始质心
• random_state：控制每次质心随机初始化的随机数种子
• n_init：整数，默认10，使用不同的质心随机初始化的种子来运行 k-means 算法的次数。最终结果会是基于 Inertia 来计算的 n_init 次连续运行后的最佳输出

max_iter & tol：让迭代停下来

当质心不再移动，Kmeans算法就会停下来。但在完全收敛之前，我们也可以使用max_iter，最大迭代次数，或者tol，两次迭代间Inertia下降的量，这两个参数来让迭代提前停下来。

• max_iter：整数，默认300，单次运行的k-means算法的最大迭代次数
• tol：浮点数，默认1e-4，两次迭代间Inertia下降的量，如果两次迭代之间Inertia下降的值小于tol所设定的值，迭代就会停下

4. 聚类算法的模型评估指标

4.1 当真实标签未知的时候：轮廓系数

在99%的情况下，我们是对没有真实标签的数据进行探索，也就是对不知道真正答案的数据进行聚类。这样的聚 类，是完全依赖于评价簇内的稠密程度（簇内差异小）和簇间的离散程度（簇外差异大）来评估聚类的效果。其中轮廓系数是最常用的聚类算法的评价指标。它是对每个样本来定义的，它能够同时衡量：

1）样本与其自身所在的簇中的其他样本的相似度a，等于样本与同一簇中所有其他点之间的平均距离

2）样本与其他簇中的样本的相似度b，等于样本与下一个最近的簇中的所有点之间的平均距离

根据聚类的要求”簇内差异小，簇外差异大“，我们希望b永远大于a，并且大得越多越好

单个样本的轮廓系数计算为：
$s=\frac{b-a}{\max (a, b)}$

公式可以被解析为：
$s=\left\{\begin{array}{ll} {1-a / b,} & {\text { if } a<b} \\ {0,} & {\text { if } a=b} \\ {b / a-1,} & {\text { if } a>b} \end{array}\right.$ 很容易理解轮廓系数范围是(-1,1)，其中值越接近1表示样本与自己所在的簇中的样本很相似，并且与其他簇中的样本不相似，当样本点与簇外的样本更相似的时候，轮廓系数就为负。当轮廓系数为0时，则代表两个簇中的样本相似度一致，两个簇本应该是一个簇。可以总结为轮廓系数越接近于1越好，负数则表示聚类效果非常差。

在 sklearn 中，我们使用模块metrics中的类silhouette_score来计算轮廓系数，它返回的是一个数据集中，所有样本的轮廓系数的均值。但我们还有同在metrics模块中的silhouette_sample，它的参数与轮廓系数一致，但返回的是数据集中每个样本自己的轮廓系数。

from sklearn.metrics import silhouette_score
from sklearn.metrics import silhouette_samples
X
y_pred
silhouette_score(X,y_pred)
silhouette_score(X,cluster_.labels_)
silhouette_samples(X,y_pred)

4.2 当真实标签未知的时候：Calinski-Harabaz Index

除了轮廓系数是最常用的，还有卡林斯基-哈拉巴斯指数（Calinski-Harabaz Index，简称CHI，也被称为方差比标准），戴维斯-布尔丁指数（Davies-Bouldin）以及权变矩阵（Contingency Matrix）可以使用

标签未知时的评估指标

• 卡林斯基-哈拉巴斯指数 sklearn.metrics.calinski_harabaz_score (X, y_pred)

• 戴维斯-布尔丁指数 sklearn.metrics.davies_bouldin_score (X, y_pred)

• 权变矩阵

  sklearn.metrics.cluster.contingency_matrix (X, y_pred)

from sklearn.metrics import calinski_harabaz_score
X
y_pred
calinski_harabaz_score(X, y_pred)

5. KMeans参数列表

6. KMeans属性列表

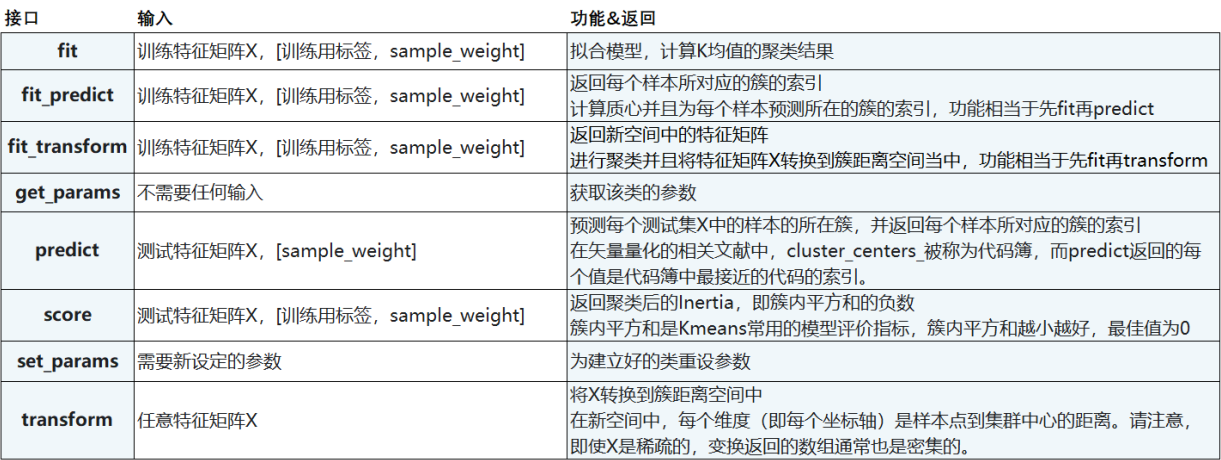
7. KMeans接口列表